Superconductivity Essentials
引言
射频(rf)超导性的许多方面,无论是基础的还是技术的,都与金属中电子的物理学深深相连。除了超导性这一迷人现象外,金属中电子的物理学对于理解热量如何穿过腔体的壁、电子如何从金属表面隧出污染rf腔体中的真空(场致发射),或如何产生二次电子以产生多打火现象都很重要。因此,简要讨论金属中传导电子的基本理论是值得的。我们推荐读者参考Ashcroft和Mermin或Reif,以获得这里提出的概念的严格发展。这里采用的直观方法使我们能够引入一些重要的物理量,这些物理量是rf超导性领域的基础,如费米能量、费米速度、伦敦穿透深度、能隙、相干长度和平均自由程。
自由电子模型
在金属行为的简单自由电子图像中,金属中原子外层的电子很容易从核心脱离并远离定义固体晶格的父离子。这些价电子自由地穿过晶格移动,负责金属的出色电导率和热导率。
经典自由电子模型的成功
在最早的方法中,称为德鲁德模型,导电电子被类比为理想气体处理。一旦从原子中释放出来,电子就自由地穿过晶格移动。正离子的库仑吸引力由一个平坦的势阱表示,电子被视为不相互作用的粒子。它们的相互排斥通过适当选择势阱的深度来全局处理。当电子穿过完美的晶体晶格时,不会受到散射。然而,当它们频繁地与晶格缺陷发生碰撞时,如缺失原子、间隙原子和化学杂质,电子确实会散射。当晶格的完美周期性被热激发的声波扰动时,电子也会被散射。这里使用“声子”这个词来提醒我们晶格振动是量子化的。晶格的热运动随温度增加。如果温度足够低,热激发的声子数量与杂质数量相比很小,以至于杂质散射占主导地位。在碰撞之间,电子自由移动的平均自由时间$\tau$,称为弛豫时间。
通过将动力学理论应用于这样的“气体”自由电子,可以构建金属的电导率($\sigma$)和热导率($\kappa$)的简单模型,我们现在将看到。如果有$n$个电子每单位体积,并且它们在电场$E$的影响下以漂移速度$v_d$移动,电流由下式给出:
$$ j = -ne\Delta v $$
由于电子在碰撞后以随机方向出现,因此碰撞前的速度对平均电子速度没有贡献。额外的速度$v_d$,简单地是加速度$\frac{eE}{m}$乘以平均时间$\tau$:
$$ \Delta v = \frac{eE}{m} \cdot \tau $$
我们还假设由于电场引起的电子速度增加与热速度相比可以忽略不计。碰撞后,由于随机热运动而失去定向速度增益。金属中的电导率方程然后变为:
$$ \mathbf{j} = \frac{ne^2 \tau}{m} \mathbf{E} \quad \text{或} \quad \mathbf{j} = \sigma \mathbf{E} $$
其中$\sigma$是由下式给出的直流电导率:
$$ \sigma = \frac{ne^2 \tau}{m} $$
通常,$n = 10^{22} \text{ cm}^{-3}$,$\tau = 10^{-14} \text{ s}$,根据观测到的电阻率。在德鲁德模型中,从经典能量均分定理得出的平均电子速度的简单估计,给出室温下$u = 10^5 \text{ cm/s}$。从这个我们可以看出电子的平均自由程,$l = v\tau$,通常是$10^{-7} \text{ cm}$。
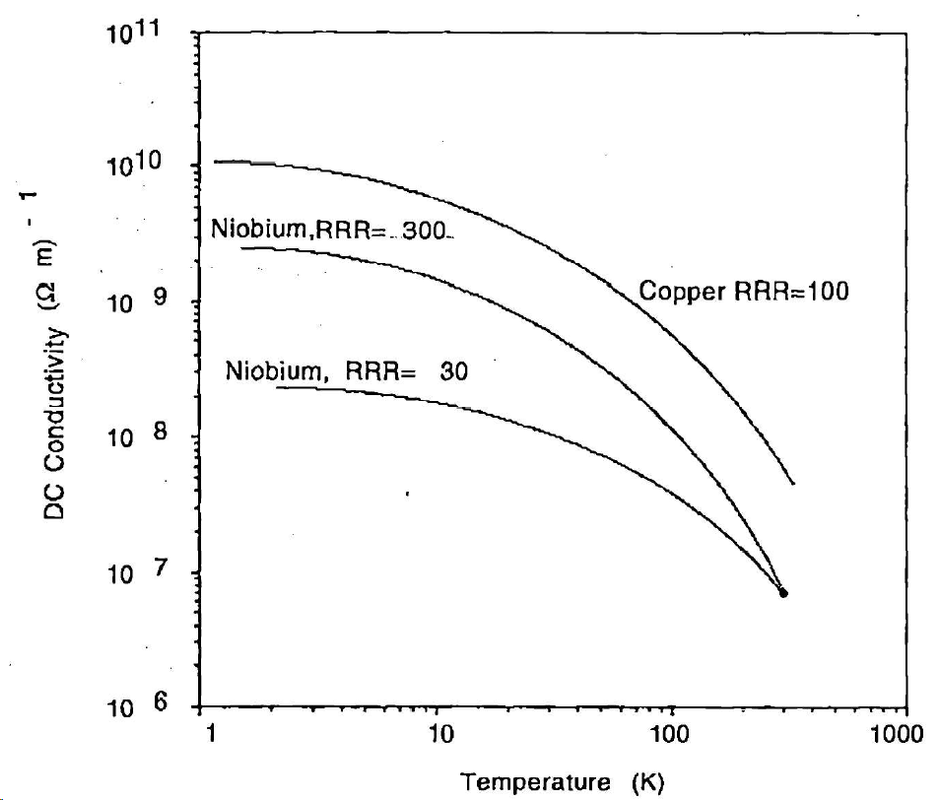
金属的电导率随着温度的降低而增加,因为晶格振动的散射项减少。但电导率的改善最终会饱和到由杂质散射决定的值。由于电子也是主要的热载体,这种限制将被证明是理解铌腔壁的热传输能力的一个同样重要的因素。例如,对于相对不纯的Nb,直流电阻率($\rho \propto 1/\sigma$)从室温值$1.4 \times 10^{-8} \Omega \cdot \text{m}$下降到其残余值的30倍。电阻率下降到残余值的30倍称为“剩余电阻比”,或RRR。高纯度铌具有更高的RRR值,理论上限为35,000,由晶格振动引起的电子散射决定。
我们现在转向热导率。在金属中,热由电子和声子传输。在低温下,单位体积的声子数量$\propto T^3$,类比于光子。(这种行为基本上反映了声子的3-D空间属性,通过声子的相空间体积。)由于$T^3$依赖性,低温下主要的热传输机制是由导电电子,即自由电子气体。在一个简单的一维模型中,有一个从高温到低温的热能净流动。热电流密度$j_g$(每面积瓦特)流过一个面积,由下式给出:
$$ j_g = - \kappa \frac{dT}{dx} $$
热电流密度可以通过考虑穿过面积的电子数量密度($n/2$),乘以电子的速度($u_r$),乘以每个电子携带的能量来估算。因此:
$$ j_g = n \cdot v_{x} \cdot E $$
从图3.3我们可以看到,来自高温区域(左侧)的电子具有能量$E[T(x - u_r\tau)]$,这比来自低温区域(右侧)的电子的能量大。请注意,电子的能量也是温度的函数。因此,从高温区域到低温区域有能量的净传输。热电流是:
$$ j_{q}=\frac{n}{2} v_{x} E\left[T\left(x-v_{x} \tau\right)\right]-\frac{n}{2} v_{x} E\left[T\left(x+v_{x} \tau\right)\right] $$
使用:
$$ E[T(x - u_x T)] - [T(x + u_x T)] = \frac{dE}{dT} \cdot 2u_x T $$
热电流变为:
$$ j_g = \frac{dE}{dT} \cdot \frac{2u_rT}{3} $$
要进入3-D情况,我们可以从气体的均分定理写出:
$$ j_g = \frac{dE}{dT} \cdot \frac{2}{3} \cdot \frac{n}{V} \cdot u_r $$
数量$\frac{dE}{dT}$与恒定体积的热容量有关:
$$ \frac{dE}{dT} = C_V $$
使用比热,以及热导率的定义,我们得到:
$$ \kappa = \frac{dE}{dT} \cdot \frac{2}{3} \cdot \frac{n}{V} \cdot u_r $$
在这个简单的动力学视角中,突出的结果是热与电导率的比率变为:
$$ \frac{\kappa}{\sigma} = \frac{m u_r^2 \tau}{3 n e^2} $$
现在我们可以进一步应用一些经典气体动力学理论的关键结果,例如温度与均方速度之间的关系,以及每个自由度的比热贡献:
$$ \frac{1}{2} m u^2 = \frac{3}{2} k_B T $$
和
$$ C_V = \frac{3}{2} N_A k_B $$
其中$k_B$是玻尔兹曼常数。在确定比热时,我们假设,如理想气体那样,电子遵循麦克斯韦-玻尔兹曼统计,即能量在$e$和$e + de$之间的电子数量由能量分布函数给出:
$$ f(e) = \frac{e^{-\frac{e}{k_B T}}}{N_A} $$
热与电导率之间的关系然后变为:
$$ \frac{\kappa}{\sigma} = \frac{3}{5} \left( \frac{k_B T}{e_F} \right) $$
经典自由电子气体模型的最大成功是这种“解释”了经验确定的维德曼-弗朗兹(WF)定律,该定律指出:
$$ \frac{\kappa}{\sigma} = L T $$
其中$L$,洛伦兹数,与温度和缺陷浓度无关。$L$也观察到对大多数金属大致相同。如果电子是金属中热和电流的主要载体,那么金属的热导率与电导率成正比。像电导率一样,金属的热导率受到电子的杂质散射限制。通过从铌中移除适当的杂质,铌腔壁的热导率增加,从而提供更好的冷却。随之而来的电导率增加,或RRR值,作为金属纯度的方便度量。RRR的正式定义是:
$$ RRR = \frac{\rho(300K)}{\rho(\text{低温(正常状态)下的残余电阻})} $$
量子力学描述
现在,经典自由电子模型出现了一个严重的问题。电子“气体”似乎根本没有贡献于金属的比热。根据能量均分定理,我们期望每个电子有额外的贡献$\frac{3}{2}k_B$,但观察到的电子贡献几乎为零。另一个与观察行为相矛盾的是,经典处理预测金属的比热与温度无关。
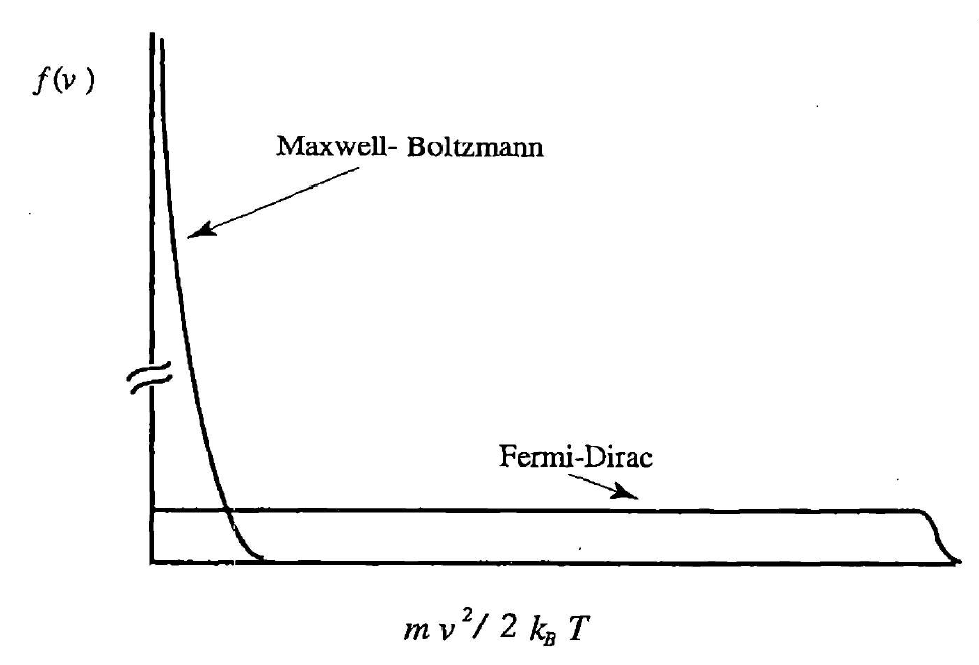
这些问题的根源在于,在经典描述中,电子速度和能量由麦克斯韦-玻尔兹曼分布给出。在量子力学描述中,电子的速度分布由费米-狄拉克函数给出,这有很大的不同。
在量子力学中,通过金属传播的电子由平面波表示。波长与速度成反比,根据德布罗意关系,$\lambda = \frac{h}{p}$。波的振幅与电子密度成比例。波通过一个完全周期性的晶体晶格而不被散射或失去其动量。电子的波函数必须满足将其限制在金属内的边界条件。这些条件导致在给定能量范围内有有限数量的状态,称为态密度,$D(\epsilon)$。这些状态的占据由泡利排斥原理控制,它引入了不同电子之间的重要统计相关性。具有平行自旋的电子避免彼此。在为$N$个电子在体积$V$中构建基态时,我们只能在每个允许的量子化能级中放置两个电子(具有相反的自旋)。接下来的两个电子必须放置在更高的能级。当我们继续放置电子时,我们使用越来越高的能量。最后两个电子放置的能量水平称为费米能级,最高能量称为费米能量,$\epsilon_F$。
我们有:
$$ \epsilon_F = \frac{\hbar^2(3\pi^2 n)^{2/3}}{2m_e} $$
这里$h$是普朗克常数,$m_e$是电子的质量。费米能级上的电子速度被称为费米速度$v_F$:
$$ v_F^{2} = \frac{2\epsilon_F}{m_e} $$
是费米速度在量子金属理论中起主要作用,而不是经典电子气体的热速度:
$$ v = \sqrt{\frac{3 k_B T}{m_e}} $$
由于泡利排斥原理,费米速度非常高,通常是光速的1%。对于铌,费米能量$E_F$是5.32 eV,费米温度$T_F = \frac{E_F}{k_B}$,是$6.18 \times 10^4$ K,费米速度$v_F$是$1.37 \times 10^6$ m/s。如果没有排斥原理,经典电子速度会低得多,即$k_B T \approx 0.02$ eV。还要注意,电子的平均自由程$l = v_F \tau$,比相邻原子之间的距离大得多。
泡利排斥原理和由此产生的费米-狄拉克(FD)统计解决了能量均分问题,并解释了为什么观察到的电子气体的比热非常低。
让我们做一个简单的电子比热推导。一个给定能量状态$\epsilon$被电子占据的概率由FD分布给出:
$$ f(\epsilon) = \frac{1}{e^{\frac{\epsilon - E_F}{k_B T}} + 1} $$
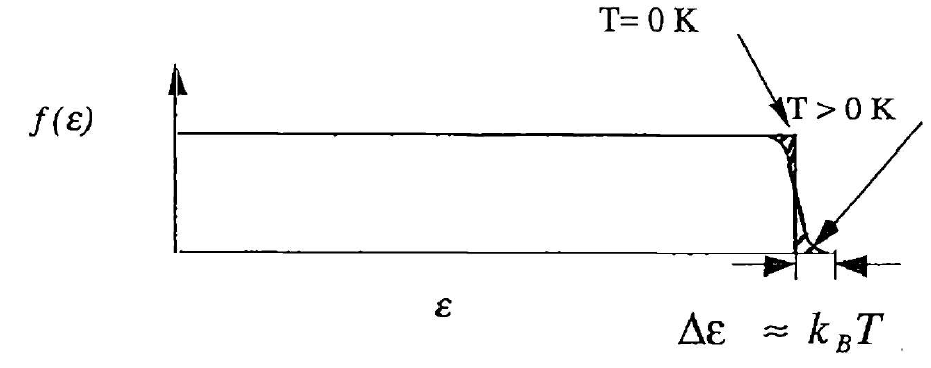
如图3.5所示,在$T = 0$ K时,FD分布是一个阶梯函数。对于$\epsilon < E_F$等于1,对于$\epsilon > E_F$等于0。在有限温度下,一些电子,那些在费米能量下方$k_B T$内的电子,被激发到费米能量上方$k_B T$内的能量状态。只有这些电子对比热和热导率有贡献。$\epsilon < E_F$的电子对金属的宏观性质影响很小,因为它们处于完全填充的状态。温度的小幅变化(与$T_F$相比)不影响这些电子,因为所有附近的州都完全满了。这些电子的平均能量也不受影响,它们不对热容量做出贡献。只有少量在区域$k_B T \approx E_F$内的电子对热容量做出贡献。在这个区域的尾部,电子能量遵循麦克斯韦-玻尔兹曼(MB)分布。因此,这个区域的每个电子对热容量贡献$\frac{3}{2}k_B$。只有总数的一小部分$\frac{k_B T}{E_F}$的电子在MB分布的尾部区域。所有这些激发的电子几乎都以费米速度$v_F$移动。每单位体积的激发电子数量是宽度$k_B T$乘以每单位体积的态密度,$D(\epsilon)$。激发能量也是$k_B T$的数量级。因此,总热能密度是:
$$ D(\epsilon)(k_B T)^2 $$
比热,即能量的温度导数,因此与$T$成正比。自由电子的确切表达式是:
$$ C_V = \frac{\pi^2}{2} \frac{k_B}{E_F} T $$
对于具有态密度$D(\epsilon)$的金属,它是:
$$ C_V = \frac{D(\epsilon) \pi^2}{2} \frac{k_B}{E_F} T $$
这里,电子比热的系数是可用电子态密度的度量。由于在普通温度下$k_B T < E_F$,电子对比热的贡献被大大抑制;在室温下,它只是总数的1%。这是费米-狄拉克统计最重要的预测之一,它是泡利排斥原理的简单结果。还要注意,比热现在是温度依赖的,与观察到的行为一致。
FD分布的另一个重要后果是,当施加电场时,大多数电子无法接受动量,因为它们在附近找不到空态。只有在分布尾部的电子才有空态可访问。
现在让我们重新审视维德曼-弗朗兹定律的基础:
$$ \frac{\kappa}{\sigma} = \frac{\mu U_F^2 \tau}{3 n e^2} $$
在量子力学处理中,我们已经看到比热因100倍的因子而减少。但由于费米速度很高,均方电子速度也因相同因子增加。因此,$v_F$和$C_V$,我们得到:
$$ \frac{\kappa}{\sigma} = \frac{3}{5} \left( \frac{k_B T}{E_F} \right)^2 $$
量子力学处理正确预测了WF定律。经典电子气体理论与WF定律之间的一致完全是偶然的。然而,讨论经典电子气体有助于理解量子力学对电子速度、平均自由程和电子温度的影响。值得注意的是,除了MB统计之外,自由电子气体图像仍然可以用来描述电导和热导以及比热的主要特征,只要FD统计取代了经典MB统计。
更一般地说,我们迄今为止在很大程度上忽略了声子,也在金属的热导率和比热中发挥作用。如前所述,声子的数量与$T^3$成比例。在低温下,电子杂质散射占主导地位,电子热导率分量,$\kappa_{electron} \propto T$。随着温度的升高,声子散射变得更加重要。电子的平均自由程,与声子数量成反比,因此将变为$\propto T^{-3}$。两种机制(杂质和声子)的散射概率可以被视为独立的。为了获得组合贡献,我们添加两个热电阻分量——即相应电导率的倒数——如下:
$$ \frac{1}{\kappa} = \frac{1}{\kappa_{electron}} + \frac{1}{\kappa_{phonon}} $$
当添加声子贡献时,金属的总比热具有以下形式:
$$ C = \gamma T + A T^3 $$
这里$A = \frac{12\pi^4 N_A k_B}{5 \Theta_D}$,其中$\Theta_D$是德拜温度,例如铌的275 K,对应于最高可能的声子能量$k_B \Theta_D \approx 0.01-0.02$ eV。晶格贡献取决于平均声子数量$\propto T^3$和平均能量$\propto T^4$。相应地,比热$\propto \frac{dE}{dT} \propto T^3$。在低温下,声子对比热的贡献远小于线性电子贡献($T$)。
超导性入门
超导性最迷人的方面是,当材料进入超导状态时,导体的电阻降为零。还没有实验能够检测到这种状态下的可测量电阻。这种奇妙现象的发现者,昂内斯,通过展示他携带的超导电线圈中的持久电流即使在他从荷兰莱顿的家到英国剑桥目的地的长途旅行中也完全稳定,戏剧性地展示了不可测量的电阻。通过仔细监测超导电线圈中的持久电流的稳定性,现已确定超导体($\rho_s$)的电阻率上限为:
$$ \rho_s < 10^{-12} \Omega \cdot m $$
作为一个实际应用,超导磁铁可以在持久电流模式下运行,无需任何低温损失,可以无限期地持续。除了无限电导率之外,超导性的另一个标志效应是完美的磁通排斥。当超导材料在外部磁场存在下冷却通过其转变温度时,磁通量被突然排出。这种壮观的磁行为,首次由迈斯纳和奥申费尔德[80]发现,称为迈斯纳效应。当我们在第4章讨论这种效应及其后果时,我们将看到它不能以麦克斯韦方程来解释。
许多材料在冷却到临界温度$T_c$以下时变得超导。除了几个纯元素外,许多化合物和合金也表现出超导性;新的高温超导体由四个或更多元素组成,也是脆性氧化物陶瓷。在元素中,铌具有最高的转变温度,$T_c = 9.2$ K。相对于所有其他元素,这种高转变温度使铌成为加速器腔最适宜的材料。更重要的是,铌可以轻松获得纯形式,并且是一种高度可加工的金属,用于形成腔体。在足够高的纯度下,铌还具有高热导率,有助于提供rf表面的热稳定性。用于超导腔的另一个元素是铅,其$T_c = 7.2$ K。
在昂内斯发现四十年后,巴丁、库珀和施里弗[81]提出了第一个超导性理论,基于电子对由于吸引势(BCS理论)的配对。这个理论在提供超导性的许多方面的微观解释以及预测新行为方面取得了巨大成功。由于导电电子与晶格原子的振动之间的相互作用,电子之间存在一个小的净吸引。一种思考这种相互作用的方式是,通过晶格的电子扭曲了晶格,变形的晶格反过来作用于第二个电子,因为正电荷积累。如图3.6所示,第一个电子穿过晶格并吸引正离子。由于它们的惯性,离子不能立即放松。最短的弛豫时间,$2\pi/\omega_D$,对应于最高可能的晶格振动频率,$\omega_D$。因此,第一个电子可以影响距离$U_F^2/\omega_D$的邻近电子,通常是几十纳米。
吸引相互作用的另一个观点是,每个电子都留下了声子的尾迹。其他电子如果穿过这个尾迹就与第一个电子相互作用。通过声子介导的电子-电子吸引因此类似于移动电荷之间的电磁相互作用,可以被认为由光子介导。另一个类比是介子介导的核子相互作用。
电子与晶格振动之间的相互作用对超导性的重要性得到了“同位素效应”的证实。给定元素的不同同位素根据以下方式具有不同的临界温度:
$$ T_c \propto \frac{1}{\sqrt{M_{atomic}}} $$
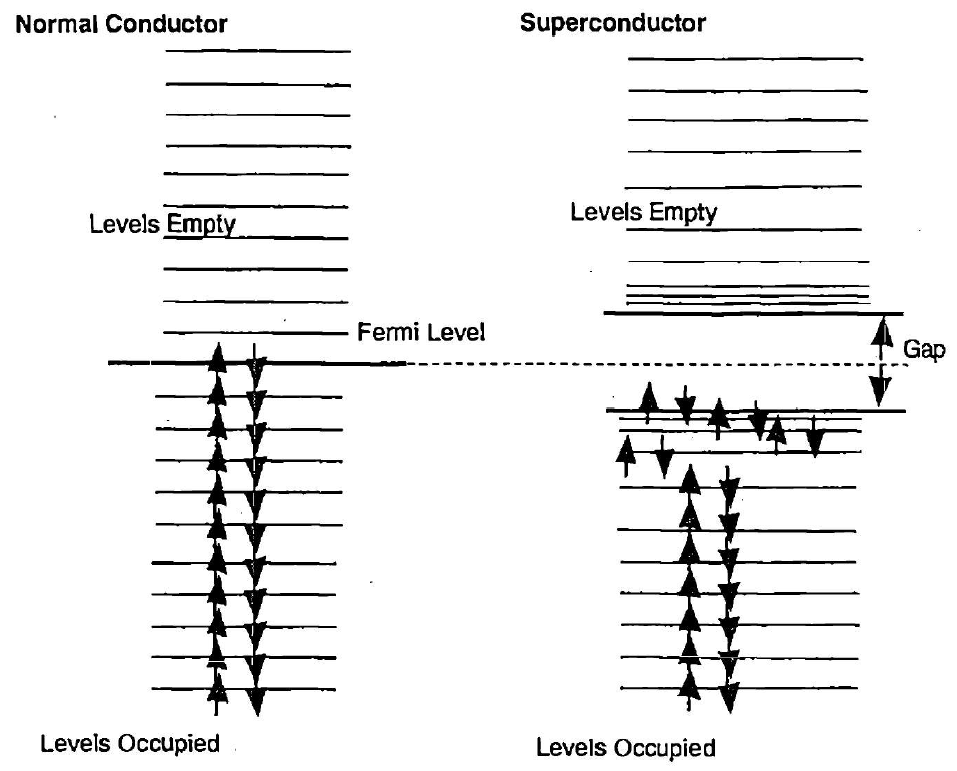
转变温度取决于组成晶格的离子的质量。这种效应由Frohlich预测,他首先提出了吸引机制。负责超导性的电子-晶格相互作用正是确定金属在高温下电阻率的相同相互作用。具有较高转变温度的超导材料,如铌和铅,确实在正常状态下具有较高的理想电阻率,因为它们强烈的电子-声子相互作用。另一方面,铜和金具有较弱的电子-声子相互作用,因此是优秀的正常导体,但没有任何超导转变。只有一小部分电子在负责超导性的相互作用中合作,那些在费米表面附近$k_B T_c h\omega_D$内的电子。这里$T_c$是转变温度,$h\omega_D$是最大声子能量的度量。在吸引相互作用存在的情况下,电子的正常费米分布变得不稳定。费米表面附近的态略有重新分布。如图3.7所示,一些电子的能量从费米水平向下推。费米水平上方可用态的分布也发生了变化。费米水平上方没有立即可用的状态。创造了一个能隙。新的基态,超导基态,比正常基态具有更低的能量。
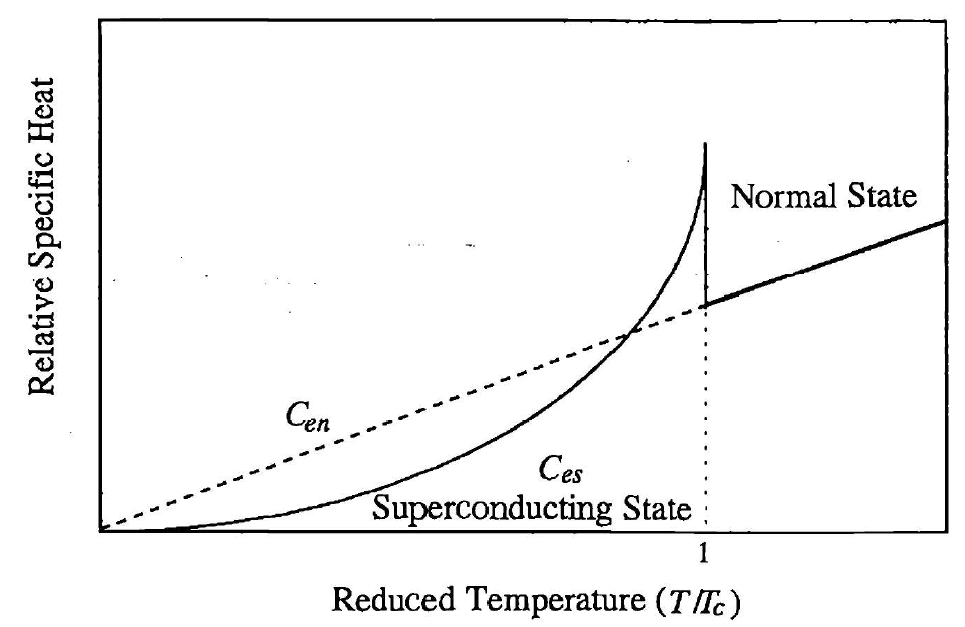
人们可以将能隙视为能量级的缺失。由于这个能隙,超导体的电子比热具有以下温度依赖性,这是其激发水平与基态由能量隙分隔的系统的特征热行为:
$$ C_{es} = \frac{A}{T} e^{-\frac{\Delta}{k_B T}} $$
如图3.8所示,超导态的电子比热与正常金属的线性电子比热非常不同。比热在$T = 0$ K以上的指数行为为能隙的存在提供了关键证据。这在图3.9中对Pb-2%In合金[85]的数据中清晰可见。测量曲线的斜率高于BCS理论的预测,因为铅的$\Delta(0)/k_B T_c$值高于BCS预测值。
正如我们稍后将看到的,微波表面电阻,$R_s(T)$的温度依赖性,是电子能级中存在间隙的另一个重要表现。
吸引相互作用的一个深远后果是电子凝聚成库珀对。BCS理论考虑了在吸引存在的情况下,费米表面附近的两个电子会发生什么,当每个电子具有的能量$e$略小于$E_F$时。在$T = 0$ K时,通过从状态中移除$E < E_F$的电子,并允许它们与能量$E > E_F$的电子形成对,基态被修改为获得更低的能量。两个电子形成一个束缚态,使它们的总能量$2e$小于$2E_F$,因为相互吸引的势能降低。
这些电子对被称为库珀对,可以被视为具有电子两倍电荷和两倍质量的新粒子。配对能量是$2\Delta(T)$。BCS理论预测了配对能量和临界温度之间的关系。在$T = 0$ K时,
$$ 2\Delta(0) = 2 \times 1.76 k_B T_c \approx 3.12 \text{ meV} $$
实际的间隙大小因材料而异,由于电子-声子相互作用强度的差异。对于铌和铅,$\Delta(0)/k_B T_c = 1.9$和$2.4$,分别。
库珀对中的电子并不是以原子中电子与质子结合的方式紧密束缚在一起。在一对中,配对电子的动量和自旋相关为$(p, \uparrow) (-P, \downarrow)$。正是这种类型的配对产生最低能量。虽然单个电子遵循费米统计,但库珀对是玻色子。泡利排斥原理不适用;相反,对遵循玻色-爱因斯坦统计。因此,所有的对都可以处于相同的量子态,具有相同的质心能量。
当电子“凝聚”成库珀对时,涉及的电子是那些在费米能量$k_B T_c$能量范围内的电子。我们可以使用这个范围来找到动量传播和配对相互作用涉及的电子的空间范围。我们有
$$ k_B T_c = \hbar \omega_p = \hbar U_F \frac{p}{m_e} $$
因此
$$ k_B T_c = \frac{\hbar^2 p^2}{2 m_e} $$
根据海森堡的不确定性原理,对的空间范围$\xi$,也称为相干长度,与动量通过$(\Delta x)(\Delta p) \sim \hbar$相关。
$$ \xi = \frac{\hbar^2}{m_e U_F} $$
相干长度是
$$ \xi = \frac{k_B T_c}{\hbar U_F} $$
对于铌$\xi = 39$ nm,对于铅$\xi = 83$ nm。大距离表明超导电子具有长程有序性,库珀对相互重叠。相干长度还给出了超导态波函数的空间范围。在正常和超导区域之间的边界上,超导态波函数从零增加到最大值超过相干长度。由于BCS理论预测了配对能量和临界温度之间的关系,因此可以用$\Delta$表示$\xi$的另一种表达式:
$$ \xi = \frac{\hbar^2}{\sqrt{2} m_e \Delta} $$
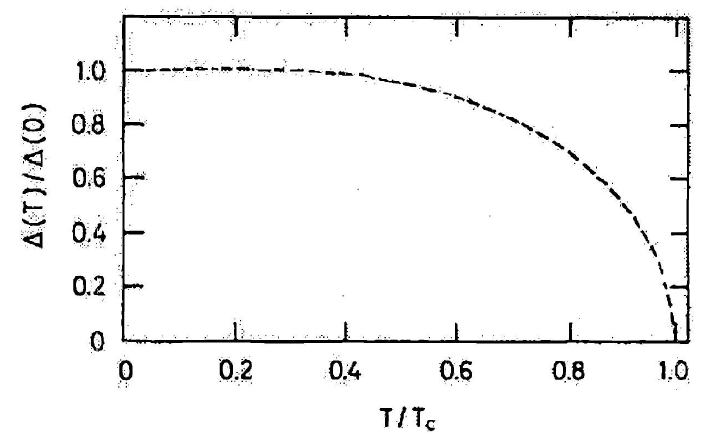
在$T > 0$ K时,超导体的激发态可以与正常态一一对应地构建。在第一激发态中,一个电子将具有动量$p$和向上自旋,但其具有向下自旋的伴侣态将为空。未配对的电子可以被视为表现为“正常”或“自由”电子。所有其他动量态仍以对的形式被占据。在这个激发态中,仍然存在能隙,但$\Delta$的值较低。$\Delta$随着$T$从0增加到$T_c$非常缓慢地下降。但在接近$T_c$时,$\Delta$急剧下降至零,如图3.10所示。对$\Delta(T)$的理论行为的有用近似由[86,87]给出:
$$ \Delta(T) = \Delta(0) \tanh \left( \frac{\sqrt{1 - (T/T_c)^2}}{1 - (T/T_c)^2} \right) $$
其中$t$是降低温度$T/T_c$。
直流和射频电阻的电气特性
可以理解超导体的零直流电阻和无限小的射频电阻,以简单的两流体模型;一种流体是配对电子的“超流体”,另一种是“自由”电子的正常流体。在$T_c$时,没有电子配对。在$T_c$以下,由玻尔兹曼因子$\exp(-\Delta/k_B T)$给出的分数是未配对的。正常电子的数量是
$$ n_{normal} = n e^{-\frac{\Delta}{k_B T}} $$
在零温度下,所有电子都配对。配对的传导电子携带超电流,电阻为零。所有对以相干的方式,统一地产生超电流。正常电流和超电流平行流动。由于超电流以零电阻流动,它可以承载整个电流,而正常电子保持惰性。
每对携带由电场施加的相同净动量。仍然存在一个能量间隙,前提是库珀对从电场中获得的能量增益小于$2\Delta$。要产生电阻,必须散射电子,即必须打破对。库珀对只有在获得超过间隙的能量时才会散射。正如我们提到的,有两种类型的散射场所:杂质(包括晶格缺陷)和声子。杂质是一个固定目标,散射不会增加对中电子的能量。因此,杂质不会散射库珀对。晶格振动也不会散射对,只要热能小于间隙,即$T < T_c$。要显示直流场中的电阻,必须停止所有现有对,并且有大量的对处于相同的量子态。因此,超导体的直流电阻正好是零。
以波图像思考零电阻也是具有启发性的。在正常金属中,电子速度高,德布罗意波长与晶格尺寸相当。电子波可以被原子尺寸的障碍物散射,例如由间隙杂质在完美晶格中造成的扰动。在超导体中,所有的库珀对由一个波集体表示。宏观德布罗意波是超导态特征的主要原因。当没有电流流动时,每个库珀对的质心(CM)处于休息状态。当超导体承载电流时,所有对都以相同的速度朝电流方向漂移。当电流($i = -n_se^2v$)流动时,它由非常大的库珀对数量承载,使得个别对的漂移速度非常低。因此,库珀对组装的波长非常长,比晶格缺陷的尺寸大得多。由于缺陷散射是不可能的,导致电阻为零。
当对从电场中获得的能量增益超过$\Delta$时,超导性将崩溃。最大(临界)电流密度由下式给出:
$$ J_c = \frac{2 e \Delta}{\hbar m_e U_F} $$
在后续章节中,我们将这种临界电流与临界磁场联系起来。
对于射频电流,超导体的表面电阻非零,尽管与正常金属相比非常小。虽然库珀对没有摩擦地移动,但它们确实有惯性。必须施加力使时间变化的电流流动。(在正常导体中,由于电子的质量,也有类似的效应,但由于散射导致的电阻淹没了由于质量产生的感抗。)由于它们的惯性,库珀对没有完美屏蔽应用场。在“皮肤深度”内存在时间变化的电场。
$$ \delta = \sqrt{\frac{2 \hbar}{\omega m_e}} $$
时间变化的电场与正常电子耦合并加速和减速它们,导致耗散。内部电流与内部电场成正比:
$$ J_{int} \propto n_{normal} E_{int} \propto n_{normal} \omega^2 $$
由于$P_{diss} \propto E_{int} J_{int}$我们发现
$$ P_{diss} \propto n_{normal} \omega^2 $$
正如我们在第2章看到的,耗散的功率可以用表面电阻来表述:
$$ P_{diss} = R_s H^2 $$
因此,由于正常电子的数量呈指数下降,我们有
$$ R_s = A \omega^2 \exp \left( -\frac{\Delta(0)}{k_B T} \right) $$
这种近似关系适用于$T < T_c/2$,当$\Delta(T)$达到渐近值$\Delta(0)$时。方程解释了超导态表面电阻的两个突出特征:
- $R_s$随着射频频率的平方增加。
- $R_s$随着温度指数下降,为$\exp(-\Delta/T)$
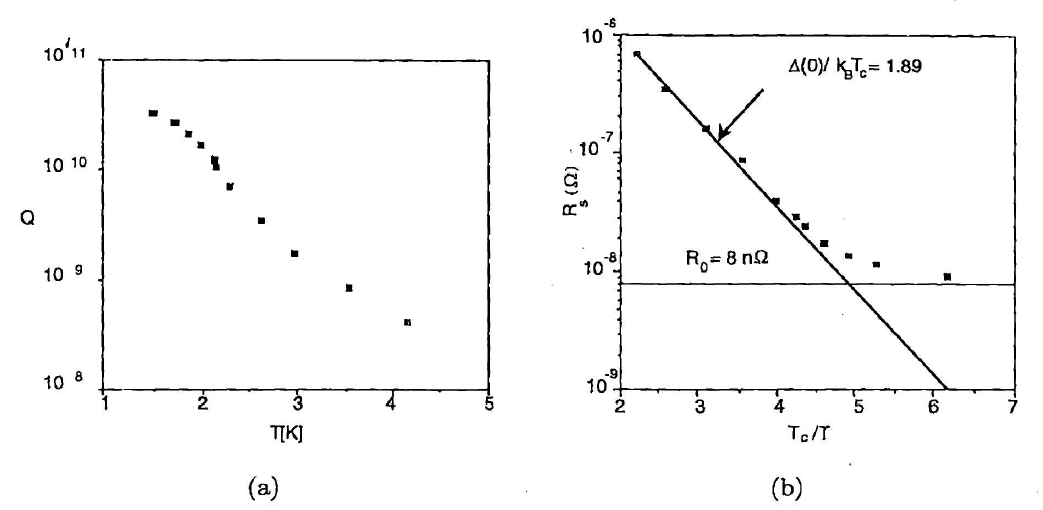
图3.11(a)显示了从$T = 4.2$ K到$T = 1.5$ K的1.5 GHz单腔体的测量$Q_o$与$T$的关系。当数据在图3.11(b)中重新绘制为$R_s$与$T_c/T$的关系时,很明显表面电阻随着
$$ R_s \propto \exp \left( -\frac{\Delta(0)}{k_B T} \right) $$
呈指数下降
指数温度依赖性,特征是间隙,已经得到了很好的证明。一般来说,方程3.48中的$A$取决于材料参数,如费米速度$U_F$,伦敦穿透深度$\Lambda_L(0)$,相干长度$\xi$和电子的平均自由程。基于BCS理论的详细表达式已经制定出来,成功地计算了$R_s$,并且存在计算机程序来执行理论所需的数值计算。
超导态中的热导率
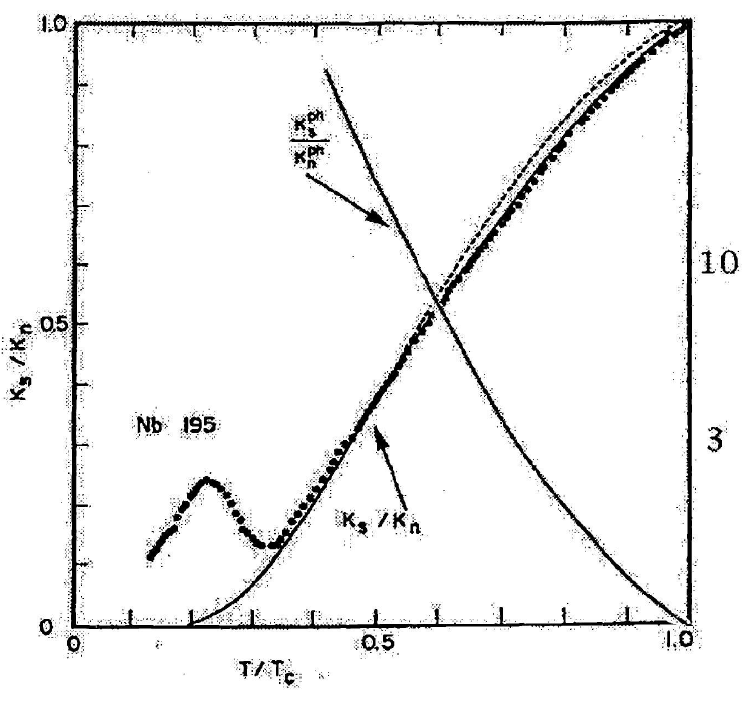
最后,我们讨论超导性对热导率的影响。正如已经提到的,低温下声子的贡献可以忽略不计,因为声子的数量$\propto T^3$。剩下的少数声子也被电子散射。因此,电子贡献在$T_c$附近占主导地位。当$T$低于$T_c$时,电子冻结成库珀对,不能传输热能,因为它们不能通过晶格振动散射。因此,低于$T_c$时,热导率急剧下降,如图3.12所示的BCS理论预测,并与$RRR = 195$的铌样品的实验结果进行比较。
根据维德曼-弗朗兹定律,该定律将正常状态的热导率与电导率联系起来,可以推导出$RRR$与4.2 K超导态热导率之间的便捷关系。
$$ RRR = \frac{4 \kappa}{\sigma} $$
库珀对的形成对铌的热导率还有另一个重要后果。随着电子的冻结,它们不再有效地散射剩下的少数声子,热导率实际上增加了。图3.12还显示了低于$T_c$的相对声子导率的理论预期增加。在足够低的温度下,声子对热导率的贡献上升到由声子的平均自由程决定的最大值。声子的重要散射场所之一是晶体晶粒的边界。对于铌,增加晶粒尺寸可以在2 K附近产生热导率峰值,通常称为“声子峰”。最后,当$T$接近零时,声子导率下降为$T^3$,这与声子密度的温度依赖性预期一致。关于铌的热导率的优秀综述可以在中找到。
原文
INTRODUCTION
Many aspects of radio frequency (rf) superconductivity, both fundamental and technological, are deeply connected with the physics of electrons in metals. Apart from the fascinating phenomenon of superconductivity, the physics of electrons in metals is important in understanding how heat is transported across the wall of the cavity, how electrons tunnel out of metal surfaces to contaminate the vacuum in the rf cavities (field emission), or how secondary electrons are generated to produce multipacting. It is therefore worthwhile to discuss briefly the fundamental theory of conduction electrons in metals. We refer the reader to Ashcroft and Mermin [3] or Reif [2] for a rigorous development of the concepts presented here. The intuitive approach adopted here allows us to stage the introduction of some of the important physical quantities that underlie the field of rf superconductivity, such as the Fermi energy, the Fermi velocity, the London penetration depth, the energy gap, the coherence length and the mean free path.
THE FREE ELECTRON MODEL
In the simple free electron picture for the behavior of a metal (Figure 3.1), electrons in the outer shells of atoms in a metal are easily detached from the core and wander away from the parent ions that define the solid lattice. These valence electrons move freely through the lattice and are responsible for the excellent electrical and thermal conductivity of metals.
Success of the Classical Free Electron Model
In the earliest approach, called the Drude model, the conduction electrons were treated by analogy to an ideal gas. Once released from the atoms, the electrons move freely through the lattice. The Coulomb attraction of the positive ions is represented by a flat potential well, and the electrons are treated as non-interacting particles. Their mutual repulsion is treated globally by suitably choosing the depth of the potential well. When traveling through a perfect crystal lattice, electrons suffer no scattering. However, they do get scattered when they suffer frequent collisions with the lattice imperfections, such as missing atoms, interstitial atoms, and chemical impurities. Electrons also get scattered by the vibrating lattice ions when the perfect periodicity of the lattice is disturbed by thermally excited sound waves. The word phonon is used here to remind us that the lattice vibrations are quantized. The thermal motion of the lattice increases with temperature. If the temperature is low enough the number of thermally excited phonons is small compared to the number of impurities, so that impurity scattering is dominant. Between collisions, electrons move freely for a mean free time $\tau$, called the relaxation time.
By applying the kinetic theory to such a “gas” of free electrons, it is possible to construct a simple model for the electrical conductivity ($\sigma$) and thermal conductivity ($\kappa$) of metals, as we shall now see. If there are $n$ electrons per unit volume, and they move with a drift velocity $v_d$ under the influence of an electric field $E$, the electrical current is given by:
$$ j = -ne\Delta v $$
Since electrons emerge from collisions in a random direction there is no contribution to the average electron velocity from the velocity before the collision. The additional velocity, $v_d$, is simply the acceleration, $\frac{eE}{m}$, times the average time $\tau$ between collisions:
$$ \Delta v = \frac{eE}{m} \cdot \tau $$
We also assume that the increment of the electron speed due to the electric field is negligible compared to the thermal speed. After collisions, the directed velocity gain is lost due to random thermal motion. The conductivity equation in a metal then becomes:
$$ \mathbf{j} = \frac{ne^2 \tau}{m} \mathbf{E} \quad \text{or} \quad \mathbf{j} = \sigma \mathbf{E} $$
where $\sigma$ is the dc electrical conductivity given by:
$$ \sigma = \frac{ne^2 \tau}{m} $$
Typically, $n = 10^{22} \text{ cm}^{-3}$, and $\tau = 10^{-14} \text{ s}$, from the observed resistivity. In the Drude model, a simple estimate for the average electron speed is made from the classical equipartition of energy theorem to give $u = 10^5 \text{ cm/s}$ for room temperature. From this we see that the electron mean free path, $l = v\tau$, is typically $10^{-7} \text{ cm}$.
The electrical conductivity of metals increases with decreasing temperature because the scattering term from lattice vibrations decreases. But the improving conductivity eventually saturates to a value determined by impurity scattering. Because electrons are also the dominant heat carriers this limitation will turn out to be an equally important factor in understanding the heat-carrying capability of the wall of a niobium cavity. For example, for relatively impure Nb, the dc resistivity ($\rho \propto 1/\sigma$) drops by a factor of 30 from its room temperature value of $1.4 \times 10^{-8} \Omega \cdot \text{m}$ to its residual value. The factor 30 by which resistivity drops to the residual value is called the “residual resistance ratio”, or RRR. High-purity niobium has higher RRR values, the theoretical limit being 35,000 [77], determined by scattering of electrons from lattice vibrations.
We turn now to thermal conductivity. In a metal, heat is transported by electrons and phonons. At low temperature, the number of phonons per unit volume $\propto T^3$, by analogy with photons. (This behavior basically reflects the 3-D properties of space via the volume of phase space for phonons.) Because of the $T^3$ dependence, the predominant mechanism for heat transport at low temperatures is by the conduction electrons, i.e., the free-electron gas. In a simple one-dimensional model, there is a net flow of heat energy from high temperature to low temperature. The thermal current density, $j_g$ (watt/area), flowing across an area is given by:
$$ j_g = - \kappa \frac{dT}{dx} $$
The heat current density can be estimated by considering the number density ($n/2$) of electrons that flow across the area, times the velocity ($u_r$) of the electrons, times the energy which each electron carries. Thus:
$$ j_g = n \cdot v_{x} \cdot E $$
From Figure 3.3 we see that an electron coming from the high-temperature region (on the left) has an energy $E[T(x - u_r\tau)]$ which is larger than the energy of an electron coming from the lower-temperature region (on the right). Note that the energy of electrons is also a function of the temperature. Thus there is a net transport of energy from the high-temperature region to the low-temperature region. The thermal current is:
$$ j_{q}=\frac{n}{2} v_{x} E\left[T\left(x-v_{x} \tau\right)\right]-\frac{n}{2} v_{x} E\left[T\left(x+v_{x} \tau\right)\right] $$
Using:
$$ E[T(x - u_x T)] - [T(x + u_x T)] = \frac{dE}{dT} \cdot 2u_x T $$
the thermal current becomes:
$$ j_g = \frac{dE}{dT} \cdot \frac{2u_rT}{3} $$
To go to the 3-D case, we can write from the equipartition theorem of the kinetic theory of gases:
$$ j_g = \frac{dE}{dT} \cdot \frac{2}{3} \cdot \frac{n}{V} \cdot u_r $$
The quantity $\frac{dE}{dT}$ is related to the heat capacity from the definition of specific heat at constant volume:
$$ \frac{dE}{dT} = C_V $$
Using the specific heat, along with the definition of thermal conductivity (Equation 3.6), we derive:
$$ \kappa = \frac{dE}{dT} \cdot \frac{2}{3} \cdot \frac{n}{V} \cdot u_r $$
In this simple kinetic view, the salient result is that the ratio of the thermal to the electrical conductivity becomes:
$$ \frac{\kappa}{\sigma} = \frac{m u_r^2 \tau}{3 n e^2} $$
Now we can further apply some of the key results of the classical kinetic theory of gases, such as the relation between temperature and mean square velocity, as well as the specific heat contribution from each degree of freedom:
$$ \frac{1}{2} m u^2 = \frac{3}{2} k_B T $$
and
$$ C_V = \frac{3}{2} N_A k_B $$
where $k_B$ is Boltzmann’s constant. In determining the specific heat we assume, as in an ideal gas, that the electrons obey Maxwell-Boltzmann statistics, i.e., the number of electrons with energy between $e$ and $e + de$ is given by the energy distribution function:
$$ f(e) = \frac{e^{-\frac{e}{k_B T}}}{N_A} $$
Using Equations 3.15 and 3.16, the relation between thermal and electrical conductivities then becomes:
$$ \frac{\kappa}{\sigma} = \frac{3}{5} \left( \frac{k_B T}{e_F} \right) $$
The greatest success of the classical free electron gas model was this “explanation” of the empirically established Wiedemann-Franz (WF) law, which states that:
$$ \frac{\kappa}{\sigma} = L T $$
where $L$, the Lorenz number, is independent of temperature and defect concentration. $L$ is also observed to be approximately the same for most metals. If electrons are the predominant carriers of both heat and electrical current in metals, then the thermal conductivity of a metal is proportional to the electrical conductivity. As with electrical conductivity, the thermal conductivity of a metal is limited by impurity scattering of electrons. We will see in Chapter 6 that by removing the appropriate impurities from niobium, the thermal conductivity of the wall of a niobium cavity increases, thereby providing better cooling. The accompanying increase in electrical conductivity, or the RRR value, serves as a convenient measure of the purity of the metal. The formal definition of RRR is:
$$ RRR = \frac{\rho(300K)}{\rho(\text{residual resistivity at low temperature (normal state)})} $$
Quantum Mechanical Description
There comes now a serious difficulty with the classical free electron model. The electron “gas” does not appear to contribute at all to the heat capacity of a metal. From the equipartition of energy theorem, we expect an additional contribution of $\frac{3}{2}k_B$ per electron, but the observed electron contribution is nearly zero. Another contradiction to observed behavior is that the classical treatment predicts that the specific heat of a metal is temperature-independent.
The source of these problems is that in the classical description the electron velocities and the energies are given by the Maxwell-Boltzmann distribution as shown in Figure 3.4. In the quantum mechanical description the velocity distribution for the electrons is given by the Fermi-Dirac function (Figure 3.4), which is vastly different.
In quantum mechanics, an electron traveling through a metal is represented by a plane wave. The wavelength is inversely proportional to the velocity according to the de Broglie relation, $\lambda = \frac{h}{p}$. The amplitude of the wave is proportional to the density of electrons. The wave passes through a perfectly periodic crystal lattice without being scattered or losing its momentum. The wave function of the electron must satisfy the boundary conditions that keep it confined within the metal. These conditions lead to a finite number of states in a given energy range, referred to as the density of states, $D(\epsilon)$. The occupation of these states is governed by the Pauli exclusion principle which introduces an important statistical correlation between different electrons. Electrons with parallel spins avoid each other. In building up the ground state for $N$ electrons in a volume $V$, we may place only two electrons (with opposite spins) in each allowed quantized energy level. The next two electrons have to be placed at a higher energy level. As we continue to place electrons we use up higher and higher energies. The energy level at which the last two electrons are placed is called the Fermi level, and the highest energy is known as the Fermi energy, $\epsilon_F$.
We have:
$$ \epsilon_F = \frac{\hbar^2(3\pi^2 n)^{2/3}}{2m_e} $$
Here $h$ is Planck’s constant and $m_e$ is the mass of the electron. The velocity of electrons at the Fermi level is referred to as the Fermi velocity $v_F$:
$$ v_F^{2} = \frac{2\epsilon_F}{m_e} $$
It is the Fermi velocity which plays the major role in the quantum theory of metals, rather than the thermal velocity of the classical electron gas:
$$ v = \sqrt{\frac{3 k_B T}{m_e}} $$
Because of the Pauli exclusion principle, the Fermi velocity is very high, typically 1% of the velocity of light. For niobium, the Fermi energy, $E_F$, is 5.32 eV, the Fermi temperature, $T_F = \frac{E_F}{k_B}$, is $6.18 \times 10^4$ K, and the Fermi velocity, $v_F$, is $1.37 \times 10^6$ m/s. Without the exclusion principle, the classical electron velocity would be much lower, i.e., $k_B T \approx 0.02$ eV. Note also that the mean free path of the electrons, $l = v_F \tau$, is very much larger than the distance between neighboring atoms.
The Pauli exclusion principle and the resulting Fermi-Dirac (FD) statistics resolve the equipartition energy problem and explain why the observed specific heat of the electron gas is very low.
Let us make a simple derivation of the electronic specific heat. The probability that a given state of energy $\epsilon$ is occupied by an electron is given by the FD distribution:
$$ f(\epsilon) = \frac{1}{e^{\frac{\epsilon - E_F}{k_B T}} + 1} $$
As shown in Figure 3.5, at $T = 0$ K, the FD distribution is a step function. It is equal to unity for $\epsilon < E_F$ and is equal to zero for $\epsilon > E_F$. At a finite temperature, some electrons, those within $k_B T$ below the Fermi energy, are excited to energy states within $k_B T$ above the Fermi energy. Only these electrons contribute to the specific heat and the thermal conductivity. The electrons with $\epsilon < E_F$ have very little effect on the macroscopic properties of a metal because they are in completely filled states. A small change in temperature (compared to $T_F$) does not affect these electrons since all the nearby states are completely full. The mean energy of these electrons is also unaffected, and they do not contribute to the heat capacity. Only the small number of electrons in the region $k_B T \approx E_F$ contribute to the heat capacity. In the tail end of this region, the electron energies obey the Maxwell-Boltzmann (MB) distribution. Therefore each electron in this region contributes $\frac{3}{2}k_B$ to the heat capacity. Only a fraction $\frac{k_B T}{E_F}$ of the total number of electrons are in the tail region of the MB distribution. All these excited electrons move with nearly the Fermi velocity $v_F$. The number of excited electrons per unit volume is the width $k_B T$ times the density of states per unit volume, $D(\epsilon)$. The excitation energy is also of the order $k_B T$. Therefore, the total thermal energy density is:
$$ D(\epsilon)(k_B T)^2 $$
The heat capacity, which is the temperature derivative of the energy, is therefore proportional to $T$. The exact expression for free electrons is:
$$ C_V = \frac{\pi^2}{2} \frac{k_B}{E_F} T $$
and for a metal with density of states $D(\epsilon)$ it is:
$$ C_V = \frac{D(\epsilon) \pi^2}{2} \frac{k_B}{E_F} T $$
Here, the coefficient of the electronic specific heat, is a measure of the available electronic density of states. Since at ordinary temperatures $k_B T < E_F$, the electronic contribution to the specific heat is greatly depressed; at room temperature it is only 1% of the total. This is one of the most important predictions of Fermi-Dirac statistics, and it is a simple consequence of the Pauli exclusion principle. Note also that the specific heat is now temperature-dependent, in agreement with the observed behavior.
Another important consequence of the FD distribution is that when an electric field is applied, most of the electrons are unable to accept the momentum because they do not find empty states in their vicinity. Only those electrons in the tail of the distribution have free states accessible.
Now let us revisit the basis of the Wiedemann-Franz law:
$$ \frac{\kappa}{\sigma} = \frac{\mu U_F^2 \tau}{3 n e^2} $$
In the quantum mechanical treatment, we have seen that the specific heat is reduced by a factor of 100. But the mean square electron velocity is also increased by the same factor, because of the high Fermi velocity. Therefore, using Equation 3.22 for $U_F$ and Equation 3.26 for $C_V$, we get:
$$ \frac{\kappa}{\sigma} = \frac{3}{5} \left( \frac{k_B T}{E_F} \right)^2 $$
The quantum mechanical treatment correctly predicts the WF law. The agreement between the classical electron gas theory and the WF law was therefore entirely fortuitous. However, it was useful to discuss the classical electron gas to appreciate the impact of quantum mechanics on electron velocity, mean free path, and electron temperature. It is remarkable that, apart from MB statistics, the free electron gas picture can still be used to describe the main features of electrical and thermal conduction as well as heat capacity, provided that FD statistics replaces the classical MB statistics.
More generally, the phonons, which we have largely ignored up to now, also play a role in both the thermal conductivity and the specific heat of a metal. As we pointed out earlier, the number of phonons is proportional to $T^3$. At low temperature, electron-impurity scattering dominates, and the electronic component of thermal conductivity, $\kappa_{electron} \propto T$. As the temperature rises, phonon scattering becomes more important. The electron mean free path, which is inversely proportional to the number of phonons, will therefore become $\propto T^{-3}$. The scattering probabilities of the two mechanisms (impurities and phonons) can be considered independently. To obtain the combined contributions we add the two thermal resistivities components—that is, the reciprocals of the respective conductivities—as follows:
$$ \frac{1}{\kappa} = \frac{1}{\kappa_{electron}} + \frac{1}{\kappa_{phonon}} $$
When the phonon contribution is added, the total specific heat of metal has the form:
$$ C = \gamma T + A T^3 $$
Here $A = \frac{12\pi^4 N_A k_B}{5 \Theta_D}$, where $\Theta_D$ is the Debye temperature, e.g., 275 K for niobium, and corresponds to the highest possible phonon energy $k_B \Theta_D \approx 0.01-0.02$ eV. The lattice contribution depends on the mean number of phonons $\propto T^3$ and the mean energy $\propto T^4$. Correspondingly, the specific heat $\propto \frac{dE}{dT} \propto T^3$. At low temperature, the phonon contribution to the specific heat is much smaller than the linear electron contribution ($T$).
ENTER SUPERCONDUCTIVITY
The most fascinating aspect of superconductivity is that the electrical resistance of a conductor goes to zero when the material enters the superconducting state. No experiment has yet been able to detect a measurable resistance in this state. The discoverer of this marvelous phenomenon, Kammerlingh-Onnes [78,79], dramatically demonstrated the unmeasurable resistance by showing that the persistent current in a loop of superconducting wire he was carrying with him was completely stable even for the long period of time it took him to travel from his home in Leiden, Holland to his destination in Cambridge, England. By carefully monitoring the stability of a persistent current in a loop of superconducting wire, the upper limit for the resistivity of a superconductor ($\rho_s$) has now been established to be:
$$ \frac{\rho_s}{\rho_n} < 10^{-12} \Omega \cdot m $$
As a practical application, superconducting magnets can be operated in the persistent current mode with no cryogenic losses for an indefinitely long period. Aside from infinite conductivity, another hallmark effect of superconductivity is perfect magnetic flux exclusion. When a superconducting material is cooled through its transition temperature in the presence of an external magnetic field, the magnetic flux is abruptly expelled. This spectacular magnetic behavior, which was first discovered by Meissner and Ochsenfeld [80], is called the Meissner effect. When we discuss this effect and its consequences in Chapter 4 we will see that it cannot be explained in terms of Maxwell’s equations.
Many materials become superconducting when cooled below a transition temperature, $T_c$. Besides several pure elements, many compounds and alloys also exhibit superconductivity; the new high-temperature superconductors comprise of four or more elements and are also brittle oxide ceramics. Among the elements, niobium has the highest transition temperature, $T_c = 9.2$ K. Relative to all other elements, this high transition temperature makes niobium the most suitable for accelerator cavities. More importantly, niobium is readily available in pure form and is a highly workable metal for forming cavities. At sufficiently high purity, niobium also has a high thermal conductivity that helps provide thermal stability of the rf surface. The other element used for superconducting cavities is lead, which has $T_c = 7.2$ K.
Forty years after the discovery by Kammerlingh-Onnes, the first theory of superconductivity was presented by Bardeen, Cooper, and Schrieffer [81], based on a pairing of electrons due to an attractive potential (the BCS theory). This theory has been enormously successful in providing a microscopic explanation for many aspects of superconductivity, as well as for predicting new behavior. Because of the interaction between the conduction electrons and the vibration of the atoms of the lattice, there is a small net attraction between the electrons. One way to think of the interaction is that an electron moving through the lattice distorts the lattice, and the deformed lattice in turn acts on a second electron because of the positive charge accumulation. As shown in Figure 3.6, the first electron passes through the lattice and attracts the positive ions. Because of their inertia, the ions cannot relax immediately. The shortest relaxation time, $2\pi/\omega_D$, corresponds to the highest possible lattice vibration frequency, $\omega_D$. Therefore the first electron can influence a neighboring electron at a distance of $U_F^2/\omega_D$, typically many tens of nanometers.
Another view of the attractive interaction is that each electron leaves behind a wake of phonons. Other electrons interact with the first electron if they travel through this wake. The electron-electron attraction, mediated by phonons, is therefore analogous to the electromagnetic interaction between moving charges, which can be considered to be mediated by photons. Another analogy is provided by the nucleon interaction as mediated by mesons.
The importance to superconductivity of the interaction between electrons and lattice vibrations is confirmed by the “isotope effect” [82,83]. Different isotopes of a given element have a different critical temperature according to:
$$ T_c \propto \frac{1}{\sqrt{M_{atomic}}} $$
The transition temperature depends on the mass of the ions comprising the lattice. This effect was predicted by Frolich [84], who first proposed the attractive mechanism. The electron-lattice interaction responsible for superconductivity is the very same interaction that determines the resistivity of metals at high temperatures. The higher transition temperature superconducting materials, such as niobium and lead, indeed have a high ideal resistivity in the normal state, because of their strong electron-phonon interaction. On the other hand, copper and gold have a weak electron-phonon interaction, and thus are excellent normal conductors, but do not show any superconducting transition. Only a small fraction of the electrons cooperate in the interaction responsible for superconductivity, those within $k_B T_c h\omega_D$ of the Fermi surface. Here $T_c$ is the transition temperature, and $h\omega_D$ is a measure of the maximum phonon energy. In the presence of the attractive interaction, the normal Fermi distribution of electrons becomes unstable. The states near the Fermi surface get redistributed slightly. As shown in Figure 3.7, some electrons have their energy pushed down from the Fermi level. The distribution of available states above the Fermi level is also altered. No states are available immediately above the Fermi level. An energy gap is created. The new ground state, the superconducting ground state, has a lower energy than the normal ground state.
One can view the energy gap as an absence of energy levels. As a result of this gap, the electronic component of the specific heat of a superconductor has the temperature dependence which is the characteristic thermal behavior of a system whose excited levels are separated from the ground state by an energy gap:
$$ C_{es} = \frac{A}{T} e^{-\frac{\Delta}{k_B T}} $$
As shown in Figure 3.8, the superconducting state electronic specific heat is quite different from the linear electronic specific heat of a normal metal. The observed exponential behavior of the specific heat above $T = 0$ K provides the crucial evidence for the existence of the energy gap. This is clearly seen in Figure 3.9 for the data for a Pb-2%In alloy [85]. The slope of the measured curve is higher than the prediction of the BCS theory because lead has a higher value for $\Delta(0)/k_B T_c$ than the BCS predicted value (see below).
As we shall see later, the temperature dependence of the microwave surface resistance, $R_s(T)$, is another important manifestation of the presence of a gap in the electronic energy levels, and therefore it exhibits a behavior very similar to that of Figure 3.9.
A profound consequence of the attractive interaction is the condensation of electrons into Cooper pairs. The BCS theory considers what happens to two electrons near the Fermi surface in the presence of the attraction when each electron has an energy $e$ infinitesimally less than $E_F$. At $T = 0$ K, the ground state is modified to give a lower energy by removing electrons from states with $E < E_F$ and allowing them to form pairs with electrons with energy $E > E_F$. The two electrons form a bound state so that their total energy $2e$ is less than $2E_F$, because of the lowering of the potential energy from the mutual attraction.
These electron pairs are called Cooper pairs which can be regarded as new particles with twice the charge and twice the mass of an electron. The pairing energy is $2\Delta(T)$. The BCS theory predicts a relation between the pairing energy and the critical temperature. At $T = 0$ K,
$$ 2\Delta(0) = 2 \times 1.76 k_B T_c \approx 3.12 \text{ meV} $$
The actual size of the gap is different from one material to another due to differences in the electron-phonon interaction strength. For niobium and lead, $\Delta(0)/k_B T_c = 1.9$ and $2.4$, respectively.
The electrons within a Cooper pair are not tightly bound to each other in the sense of electrons to protons within an atom. In a pair, the momenta and spin of the paired electrons are correlated as $(p, \uparrow) (-P, \downarrow)$. It is this type of pairing which yields the minimum energy. Although individual electrons obey Fermi statistics, a Cooper pair is a boson. The Pauli exclusion principle does not apply; instead the pair obeys Bose-Einstein statistics. Therefore all the pairs can be in the same quantum state with the same center-of-mass energy.
When the electrons “condense” into Cooper pairs, the electrons involved are those within an energy range $k_B T_c$ of the Fermi energy. We can use this range to find the momentum spread and the spatial extent of the electrons involved in the pairing interaction. We have
$$ k_B T_c = \hbar \omega_p = \hbar U_F \frac{p}{m_e} $$
Therefore
$$ k_B T_c = \frac{\hbar^2 p^2}{2 m_e} $$
According to Heisenberg’s uncertainty principle, the spatial extent of the pair, $\xi$, also known as the coherence length, is related to the momentum via $(\Delta x)(\Delta p) \sim \hbar$.
$$ \xi = \frac{\hbar^2}{m_e U_F} $$
From Equation 3.37 and Equation 3.38, the coherence length is
$$ \xi = \frac{k_B T_c}{\hbar U_F} $$
For niobium $\xi = 39$ nm and for lead $\xi = 83$ nm. The large distance indicates that the superconducting electrons possess long-range order and that the Cooper pairs overlap each other. The coherence length also gives the spatial extent of the superconducting state wavefunction. At the boundary between a normal and a superconducting region, the superconducting state wavefunction increases from zero to the maximum value over the coherence length. Since the BCS theory predicts a relation between the pairing energy and the critical temperature, another expression for $\xi$ can be obtained in terms of $\Delta$:
$$ \xi = \frac{\hbar^2}{\sqrt{2} m_e \Delta} $$
At $T > 0$ K, the excited state of a superconductor can be constructed in a one-to-one correspondence with the normal state. In the first excited state, one electron would have momentum $p$ and spin up, but its partner state with spin down would be unoccupied. The unpaired electron can be considered to behave as a “normal” or “free” electron. All other momentum states would still be occupied in pairs. In this excited state an energy gap still exists but the value of $\Delta$ is lower. $\Delta$ drops very slowly as $T$ increases from 0 to $T_c$. But near $T_c$, $\Delta$ drops precipitously to zero, as shown in Figure 3.10. A useful approximation to the theoretical behavior for $\Delta(T)$ is given by [86,87]:
$$ \Delta(T) = \Delta(0) \tanh \left( \frac{\sqrt{1 - (T/T_c)^2}}{1 - (T/T_c)^2} \right) $$
where $t$ is the reduced temperature $T/T_c$.
ELECTRICAL PROPERTIES, DC AND RF RESISTANCE
One can understand the zero dc resistance and the infinitesimally low rf resistance of a superconductor in terms of a simple two-fluid model; one fluid is a “superfluid” of paired electrons, and the other is a normal fluid of “free” electrons. At $T_c$, none of the electrons are paired. Below $T_c$, a fraction given by the Boltzmann factor, $\exp(-\Delta/k_B T)$, are unpaired. The number of normal electrons is
$$ n_{normal} = n e^{-\frac{\Delta}{k_B T}} $$
At zero temperature all the electrons are paired. The conduction electrons which are paired carry a supercurrent with zero resistance. All the pairs behave coherently, in unison, to produce a supercurrent. The normal current and the supercurrent flow in parallel. Since the supercurrent flows with zero resistance, it can carry the entire current, while the normal electrons remain inert.
Each pair carries the same net momentum imparted by the electric field. There is still an energy gap, provided that the energy gain of the Cooper pair from the electric field is less than $2\Delta$. To produce resistance, electrons have to be scattered, i.e., pairs have to be broken up. Cooper pairs only scatter if they gain more energy than the gap. As we mentioned, there are two types of scattering sites: impurities (including lattice imperfections) and phonons. An impurity is a fixed target and scattering will not increase the energy of the electrons in the pair. Therefore impurities will not scatter Cooper pairs. Lattice vibrations will also not scatter pairs as long as the thermal energy is smaller than the gap, i.e., $T < T_c$. To show resistance in a dc field, all existing pairs have to be stopped, and there are a very large number of pairs in the same quantum state. Therefore the dc resistance of a superconductor is exactly zero.
It is also illustrative to think about zero resistance in terms of the wave picture. In a normal metal, the electron velocity is high and the de Broglie wavelength turns out comparable to the lattice dimension. The electron waves can be scattered by obstacles of atomic dimensions, such as the disturbance in the perfect lattice created by interstitial impurities. In a superconductor, all the Cooper pairs are represented collectively by one wave. The macroscopic de Broglie wave is the main reason for the hallmark features of the superconducting state. When there is no current flow the center of mass (CM) of each Cooper pair is at rest. When the superconductor carries current, all the pairs drift with one and the same velocity in the direction of the current. When the current ($i = -n_se^2v$) flows, it is carried by a very large number of Cooper pairs so that the drift velocity of the individual pairs is very low. Hence the wavelength of the Cooper pair assembly is very large, much larger than the dimensions of the lattice imperfections. Scattering by imperfections is impossible, leading to zero resistance.
When the energy gain of the pairs from the electric field exceeds $\Delta$, superconductivity will break down. The maximum (critical) current density is given by:
$$ J_c = \frac{2 e \Delta}{\hbar m_e U_F} $$
In a later chapter we will relate this critical current to the critical magnetic field.
For rf currents, the surface resistance of a superconductor is nonzero, although it is very small compared to a normal metal. While the Cooper pairs move without friction, they do have inertia. Forces must be applied to make the time-varying current flow. (In a normal conductor, there is a similar effect arising from the mass of the electrons, but the resulting inductive impedance is overwhelmed by the resistance due to scattering.) Because of their inertia, the Cooper pairs do not screen the applied field perfectly. A time-varying electric field is present in the skin layer. It is induced by the time-varying magnetic surface field which penetrates into the “skin depth” (see below),
$$ \delta = \sqrt{\frac{2 \hbar}{\omega m_e}} $$
The time-varying electric field couples to the normal electrons to accelerate and decelerate them, leading to dissipation. The internal current is proportional to the internal electric field:
$$ J_{int} \propto n_{normal} E_{int} \propto n_{normal} \omega^2 $$
Since $P_{diss} \propto E_{int} J_{int}$ we find
$$ P_{diss} \propto n_{normal} \omega^2 $$
As we saw in Chapter 2, the dissipated power can be couched in terms of a surface resistance:
$$ P_{diss} = R_s H^2 $$
Therefore, since the number of normal electrons decreases exponentially, we have
$$ R_s = A \omega^2 \exp \left( -\frac{\Delta(0)}{k_B T} \right) $$
This approximate relation is valid for $T < T_c/2$ when $\Delta(T)$ has reached the asymptotic value $\Delta(0)$, as shown in Figure 3.10. Equation 3.48 explains two of the prominent features of the superconducting state surface resistance:
- $R_s$ increases with the square of the rf frequency.
- $R_s$ decreases exponentially with temperature, as $\exp(-\Delta/T)$
Figure 3.11(a) shows the measured $Q_o$ versus $T$ for a 1.5 GHz single-cell cavity from $T = 4.2$ K to $T = 1.5$ K. When the data are replotted in Figure 3.11(b) as $R_s$ versus $T_c/T$, it is clear that the surface resistance decreases exponentially as
$$ R_s \propto \exp \left( -\frac{\Delta(0)}{k_B T} \right) $$
The exponential temperature dependence, characteristic of the gap, has been well demonstrated. In general, $A$, in Equation 3.48 depends on the material parameters, such as the Fermi velocity $U_F$, the London penetration depth $\Lambda_L(0)$ (see Chapter 4), the coherence length $\xi$, and the mean free path of electrons. Detailed expressions based on the BCS theory have been worked out to successfully calculate $R_s$, and computer programs exist to carry out the required numerical computations called for by the theory.
THERMAL CONDUCTIVITY IN THE SUPERCONDUCTING STATE
Finally we discuss the influence of superconductivity on the thermal conductivity. As already mentioned, at low temperatures the contribution of the phonons is negligible, because the number of phonons $\propto T^3$. The few remaining phonons are also scattered by electrons. Therefore the electronic contribution dominates near $T_c$. As $T$ decreases below $T_c$, electrons freeze out into Cooper pairs which cannot transport thermal energy, as they cannot be scattered by lattice vibrations. Therefore, below $T_c$, the thermal conductivity drops sharply, as shown by the predictions [88] of the BCS theory in Figure 3.12 and compared to the experimental results [89] for a niobium sample of $RRR = 195$.
From the Wiedemann-Franz law, which relates the normal state thermal conductivity to the electrical conductivity, a convenient relationship can be derived between the $RRR$ and the superconducting state thermal conductivity at $4.2$ K.
$$ RRR = \frac{4 \kappa}{\sigma} $$
The formation of Cooper pairs has another important consequence on the thermal conductivity of niobium. As electrons freeze out, they are no longer effective scatterers for the few remaining phonons, and the thermal conductivity actually increases. Figure 3.12 also shows the theoretically expected increase of relative phonon conductivity below $T_c$. At sufficiently low temperature the phonon contribution to the thermal conductivity rises to a maximum determined by the mean free path of the phonons. One of the important scattering sites for phonons are the boundaries of the crystal grains. For niobium, increasing the grain size can produce a peak in the thermal conductivity near $2$ K [91], normally referred to as the “phonon peak” (Figure 3.12). Finally, as $T$ approaches zero the phonon conductivity falls as $T^3$, as expected from the temperature dependence of the phonon density. An excellent review of the thermal conductivity of niobium can be found in [91,763].