约瑟夫森效应
约瑟夫森(Josephson)效应(以下简称为约氏效应)是超导体的一种宏观量子效应,所以在讨论约氏效应以前,有必要先简单介绍一下超导现象和宏观量子效应。
一、超导和宏观量子效应
早在1911年荷兰的昂尼斯(Onnes)就在实验中发现了超导现象,他发现的超导体是水银,以后又陆续发现某些金属(如Nb、Pb、V、Al,Zn、*等)和合金(如NbsGe、Nb,Ga、NbaAI、NbsAl,Ge等等)也具有超导性,目前已发现了上千种超导体。这些超导体在低于某一临界温度Tc以后(Tc一般都很接近于绝对零度,目前已知Tc最高的是Nb3Ge,其Tc=23.4K),其电阻率突然降到零,成为超导电状态。在超导电状态下,超导体的电阻为零,故电流流过超导体不产生电压降,也没有损耗。当温度升高到大于某个值以后,超导电状态消失,转变为具有电阻的正常导电状态。
关于超导的微观机理的探索延续了将近半个世纪,直到1957年才由巴丁(J.Bardeen)、库珀(L.N.Cooper)和施瑞弗(J.R.Schrieffer)建立起系统的理论),即著名的BCS理论。BCS理论相当复杂,需要用到量子力学,量子统计,固体物理等基确理论,远远超出本书的范围,这里只能作一些定性的简单概念的介绍。
BCS理论认为超导体中参与导电的不是单个电子,而是所谓“库珀电子对”(Cooper pairs),这是解释超导现象的关键概念。库珀电子对是超导电流的载流子,它是由两个电子配对而成的,带有两倍电子电荷(-2e)。组成库珀电子对的两个电子彼此隔开相当大的距离,通过某种长程相互作用束在一起。本来电子与电子之间的静电力是斥力,不可能由此而配成对,但金属中的自由电子除了静电力以外,还可以通过晶格点阵的振动而产生长程相互作用(即电子之间彼此交换“虚声子”)。在满足一定条件下,两个电子之间通过这种电子一晶格相互作用所产生的长程吸引力,可以超过其静电斥力,从而将一对动量相反、自旋反平行的电子结合起来,形成束缚态,这就是库珀电子对,简称为库珀对。库珀对中的两个电子间的平均距离大约为10^-10厘米数量级,称为相干长度ξ,而金属的晶格间距一般为几个埃(1Å=10^-10厘米),故比晶格间距大几千倍。在超导体中直径为ξ的球体内包含若大约10^5以上的库珀对,因此相邻库珀对的质心之间的平均距离,远小于同一库珀对中两个电子之间的平均距离。所以在超导体中有大量的库珀对彼此相互交叉重叠,一直延伸扩展到整块超导体,形成一种“凝聚态”,表现出宏观量子效应。
在普通金属中参与导电的是电子,电子的自旋为1/2。对于自旋为1/2的费米子具有完全相同的量子状态,描述其状态的诸量子数中至少有一个是不同的。电子是费米子,应遵守泡里不相容原理,在普通(非超导)金属中,尽管温度接近于绝对零度,其导带中的电子仍按泡里原理分别处于不同的态,其动量具有一定的统计分布。这种分别具有不同的动量各自作分散运动的电子,很容易受到晶格点阵散射的影响。当有电流流通时,由于这种晶格点阵散射的影响,使得电子的定向有序运动部分地转化为无序的热运动,这就产生了能量损耗,其宏观表现就是金属具有一定的电阻。所以普通(非超导的)金属的电阻虽然随温度下降而减小,但并不会等于零。
处于超导状态的超导体中的情形则完全不同,超导电流的载流子是库珀对,库珀对中的两个电子的自旋互相反平行而抵消。因此库珀对的自旋是0的整数倍,属于玻色子,服从玻色统计。玻色子不遵守泡里不相容原理,许多玻色子可以处于同一状态,形成高度简并态,因而就有可能用同一个波函数来描述所有库珀对的运动状态。实际上,在超导体中所有的库珀对确实都具有相同的波函数,其质心动量全都一样。无超导电流时,所有库珀对的质心动量全为零,当有超导电流流通时,所有库珀对都具有相同的动量。之所以出现这种情况,还可以从另一方面得到解释。前面说过,整个超导体中的所有库珀对不是孤立的,而是彼此重叠交叉形成一个凝聚态。在这种凝聚态中所有组成库珀对的电子都不是自由的,而是被一种长程力所支配,互相约束成为一个整体,其中任何一个电子都不能单独行动,而只能作整体运动。在这种高度组织化的有序状态中,其中的库珀对的动量都具有相同的值,就可以理解了。总之,只要超导体中的库珀对不被拆散,其动量就不受晶格点阵热运动的散射影响而始终保持同一,所以由这些库珀对作为载流子的超导电流就没有能量损耗,宏观上就呈现为零电阻。这样就定性地解释了超导电现象。
在超导状态下,库珀对所具有的能量比正常电子的能量低,两者之间有一个能量间隙2ΔE,这个2ΔE就是库珀对的结合能,也就是拆散一对库对所需的能量。BCS理论估计出在0K时2ΔE~3.5kTc(k是玻尔兹曼常数,Tc是超导体的转变温度)。当T<Tc时,由于在能量上有利于电子结成库珀对,故大部分电子都结合成库珀对(当然不是全部电子都结合成库珀对,总还有一些自由电子,两者以一定的比例处于热平衡),这就是超导状态。随着温度T的增加,库珀对的结合能2ΔE减小。当T>Tc以后,2ΔE=0,能量间隙不复存在,库珀对就全部被拆散了,这时金属就恢复到正常导电状态。这样就定性地解释了在Tc处的电阻的突然变化。
根据量子力学,微观粒子的状态由其波函数描述。在超导体中,由于其中所有的库珀对的质心动量都相同,且由于库珀对在空间至相重叠交叉,遍及整块超导体形成凝聚态,所以整块超导体中所有的库珀对的量子状态,都可以用一个“公共波函数”来描述,可写成:
$$ \Psi = \sqrt{n} e^{i\phi} $$
其中n是库珀对的体密度(单位体积内的库珀对数),φ是库珀对的公共相位。
我们知道在量子力学中,波函数一般是描述微观粒子的微观状态的,但在凝聚态中,上述公共波函数却描述了整个超导体中所有库珀对的宏观状态,所以这是一种“宏观量子态”。与这种宏观量子态有关的一些量子效应,将以宏观的规模直接显示出来,称为“宏观量子效应”。宏观量子效应除了超导电性以外,还有“超流动性”和“磁通量子化”等,都已在实验中观察到。这种宏观量子效应不仅具有重要的理论意义,而且蕴含着巨大的实用潜力。
二、约瑟夫森效应
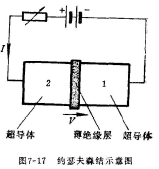
1962年约瑟夫森(B.D.Josephson)从理论上预言,当两块超导体为一薄的绝缘层所隔开如图7-17所示时,将出现“超导隧道效应”。这个预言,1963年为实验所证实,被称为“约瑟夫森效应”,简称为约氏效应。
约氏效应包括以下三个方面的内容:
- 当跨越结区(这里的绝缘层就是约瑟夫森结)的电压V=0时,有直流超导电流流过结区,这是一种超导隧道效应,称为直流约氏效应。
- 当直流超导电流I超过某一临界值Ic以后,结区出现直流电压同时有交流超导隧道电流流过,其频率由决定于结区电压V,称为约瑟夫森频率,由于$ h $是普朗克常数,$ e $是电子电荷,$ V $是结区电压,因此当V为微伏到毫伏数量级范围内时,相应的频率在微波到亚毫米波段。这就是交流约氏效应,实际上是种微波效应。
- 改变结区附近的磁场,可以控制流过结区的超导隧道电流。
对于微波技术来说,感兴趣的主要是交流约氏效应,它在微波技术中有重要的应用。
下面我们主要讨论有关这方面的问题。
约瑟夫森原来的理论推导是比较复杂的,这里不可能详细介绍。后来费曼(R.P.Feynman)对约氏效应作出了一个简单推导。费曼的推导虽然很简单,但物理概念清楚,而且同样可以得出约氏效应的两个基本方程。对于工程应用而言,费曼的唯象理论已经足够了,下面介绍费曼理论的主要内容。
考虑如图7-17所示的约氏结,如果中间的绝缘层足够厚,两边的两块超导体就被它所隔离,互相独立,可以分别考虑。这时设1、2两块超导体中的库珀对分别处于能量为E1和E2的定态,它们的“公共波函数”和应分别满足如下之定态薛定谔(Schrödinger)方程:
$$ \frac{\hbar}{i} \frac{\partial \psi_1}{\partial t} = E_1 \psi_1 $$
$$ \frac{\hbar}{i} \frac{\partial \psi_2}{\partial t} = E_2 \psi_2 $$
这时由于两块超导体互相隔离,其中的库珀对彼此完全分开,不存在耦合,当然不会有超导电流流过绝缘层。这是一种极端情况。另一种极端情况是,如果不存在绝缘层,则1、2两块超导体合二为一,其中的库珀对的公共波函数相同,ψ1=ψ2。这时将有通常的直流超导电流流过超导体,但并不存在超导隧道效应。
约氏效应是在1、2两块超导体之间存在着弱耦合,即中间的绝缘层足够薄(实验表明绝缘层的厚度约为10~30埃)时才发生的。这种薄的绝缘层对于它两边的超导体中的库珀对而言,相当于一个很窄的势垒。在这种情况下,库珀对可以通过隧道效应穿过势垒,这就在1、2两块超导体之间提供了某种弱耦合。这时式(7-85)的右方应添加相应的耦合项。费曼建议以下列耦合方程组唯象地描述存在耦合时的量子效应:
$$ \frac{\hbar}{i} \frac{\partial \psi_1}{\partial t} = E_1 \psi_1 + \Delta \psi_2 $$
$$ \frac{\hbar}{i} \frac{\partial \psi_2}{\partial t} = E_2 \psi_2 + \Delta \psi_1 $$
这里的耦合系数Δ表征耦合度的一个实参量,决定于结区的情况。根据式(7-82),设1、2两块超导体中库珀对的公共波函数分别为:
$$ \psi_1 = \sqrt{n_1} e^{i\phi_1} $$
$$ \psi_2 = \sqrt{n_2} e^{i\phi_2} $$
代入式(7-86)中,分别取其虚部和实部,不难得到:
$$ \frac{\partial \phi_1}{\partial t} = -\frac{2eV}{\hbar} $$
$$ \frac{\partial \phi_2}{\partial t} = \frac{2eV}{\hbar} $$
实部:
$$ \frac{\partial n_1}{\partial t} = -\frac{2eV}{\hbar} \sin(\phi_1 - \phi_2) $$
$$ \frac{\partial n_2}{\partial t} = \frac{2eV}{\hbar} \sin(\phi_1 - \phi_2) $$
以上a、b两式给出:
$$ \frac{\partial \phi_1}{\partial t} = \frac{\partial \phi_2}{\partial t} $$
这说明库珀对可以穿过势垒,在1、2两块超导体之间迁移,这就是流过结区的超导隧道电流。但是由于外电路是通过电源连通的,所以库珀对并不会因迁移而在结区的一边积聚起来。这种迁移将为外电路的反向迁移所补偿,因此仅使两块超导体中的库珀对密度n1、n2有一个微小的起伏,故近似地有:
$$ n_1 \approx n_2 $$
设结区电压为V,每个库珀对带有电荷-2e,因此库珀对穿过结区时其能量改变E1-E2=-2eV。
综上所述,根据式(7-88a)、(7-88b)两式,可得流过结区的超导隧道电流为:
$$ I = -2e \frac{\partial \phi}{\partial t} \sin(\phi_1 - \phi_2) = I_c \sin(\phi_1 - \phi_2) $$
其中S为结区之截面积,而:
$$ I_c = \frac{2e \Delta \sqrt{n_1 n_2}}{\hbar} $$
0=φ2-φ1。
再利用式(7-89)和式(7-90),从式(7-88c)、(7-88d)可得:
$$ \frac{\partial \phi}{\partial t} = \frac{2eV}{\hbar} $$
将上式代入式(7-91a)中,就得到约氏结电流I与电压V之间的关系为:
$$ I = I_c \sin(\frac{2eV}{\hbar}t + \phi) $$
下面我们利用上述理论来解释观察到的约氏效应。
- 设结区电压V=0,式(7-94)给出:
$$ I = I_c \sin(\phi) $$
这里隐含着结两边的库珀对的动能相等的假设,这一假设是符合实际情况的。I0不随时间而变,I0即为约氏效应(一)的零电压直流超导隧道电流,这就解释了直流约氏效应。
- 设结区电压V=V0,V0与时间无关,这时式(7-94)给出:
$$ I = I_c \sin(\frac{2eV_0}{\hbar}t + \phi) $$
其中:
$$ \frac{2eV_0}{\hbar} = f_J $$
就是前面曾提到的约瑟夫森频率。式(7-96)表明当结上加有直流电压V0时,有交流电流流过结区,这就解释了交流约氏效应。更重要的是式(7-84)表明理论推得的约瑟夫森频率与实验观察到的结果定量相符合。
注意到式(7-84)可以写成:
$$ 2eV_0 = hf_J $$
上式左方是带有-2e电荷的库珀对通过电压为V0的结区时失去的能量,由于是超导态,失去的这部分能量并不是以热辐射的形式释放,而是以频率为f_J的单色相干电磁波的形式放出。上式右方恰好是频率为f_J的一个量子的能量,这里的数字因子2,表明超导电流的载流子确实是带有二倍电子电荷的库珀对。
此外费曼还导出了存在磁场时的有关公式,可以解释约氏效应(三)。
三、弱耦合的具体形式
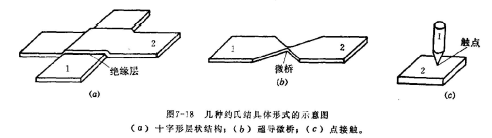
从以上分析可知,约氏效应的本质在于两块超导体之间存在弱耦合,耦合的强弱可以用流过结区的电流来表征,一般认为Ic在10^-10~10^-9安范围内属于弱耦合,典型值是毫安级。前面介绍过的薄绝缘层只是弱耦合的一种具体形式,此外还有其他各种形式。图7-18中给出了几种常用的弱耦合具体形式的示意图,这些都可以用来产生约氏效应。
- 十字形层状结构:由两条互相垂直的超导带(一般为铌Nb膜)重叠而构成,中间夹有一层氧化薄膜,形成所需的绝缘层。这种结构的特性比较稳定,但由于绝缘层很薄,结电容大,故微波阻抗很低,很难与外电路的传输线相匹配,所以这种结的微波效率不高。
- 超导微桥:是在宽度为毫米级的超导带中收缩成为一个尺寸为微米级的狭区——微桥。微桥为其两侧的超导带提供了弱耦合。这种结构便于与微带相连接。
- 点接触:是一个以化学腐蚀方法弄尖的直径为1微米左右的超导针尖(Nb针),以一定的压力压在另一块超导板上构成点接触。点接触的触点可以是金属直接相连,也可以经过一定的氧化处理。这种结构的特点是结的参量可以通过改变压力加以调整。同时由于是开放式结构,微波阻抗高,容易获得匹配。其缺点是特性不够稳定。
此外还有一些其他类型的结构,这里不再列举。在工艺上如何制造出稳定可靠,重复性好的约氏结,仍是一个尚未完全解决的问题,有待于进一步研究。
约瑟夫森效应器件中的超导体,目前常用的是采用液氮冷却到约3K的铌。