Literature Review of Calibration of superconducting radio-frequency cavity forward and reflected channels based on stored energy dynamics
基于超导腔内部储能变化校准前向和反射系数
本文提出了一种新的方法,用于校准超导射频(SRF)腔体的正向和反射信号。该方法基于能量守恒定律,通过全局非线性最小二乘优化来克服现有方法的局限性。该方法在L波段超导谐振器上进行了测试,其负载品质因数为$ 4.6 × 10^6 $和$ 2.8 × 10^7 $。
引言
- 介绍了超导射频(SRF)腔体状态估计对于直线粒子加速器高效运行的重要性。
- 讨论了射频信号测量链中的系统误差,特别是由方向耦合器的有限隔离度引起的正向($V_F$)和反射($V_R$)信号的交叉耦合效应。
能量守恒与品质因数的关系
$$ P_{cryo} = \frac{U}{\omega_0 Q_0} $$
其中 $P_{cryo}$ 是在低温系统中耗散的功率,$U$ 是RF腔体内存储的电磁能量,$\omega_0$ 是腔体的共振角频率,$Q_0$ 是腔体的无载品质因数。
半带宽与品质因数的关系
$$ \omega_{1/2} = \frac{\omega_0}{2} \sqrt{\frac{1}{Q_0} + \frac{1}{Q_{ext}}} = \frac{\omega_0}{2Q_L} $$
其中 $Q_{ext}$ 是外部品质因数,描述了超导腔与传输线之间的耦合强度,$Q_L$ 是负载品质因数。
驱动RF所需的功率
$$ P_{RF} = \frac{|V_P|^2}{4 r Q_Q L} \left( \frac{1}{1 + \left(\frac{r Q_L I_b}{|V_P|}\right)^2} + \Delta \omega^2 \right) $$
其中 $V_P$ 是加速电压或校准探针信号,$r/Q$ 是特征阻抗,$I_b$ 是束流电流,$\Delta \omega$ 是腔体失谐。
校准矩阵
$$ V_F = a V_{mF} + b V_{mR} $$
$$ V_R = c V_{mF} + d V_{mR} $$
其中 $V_F$ 和 $V_R$ 是校准后的正向和反射信号,$V_{mF}$ 和 $V_{mR}$ 是测量的正向和反射信号,$a, b, c, d$ 是信号校准参数。
能量守恒的优化问题
$$ \frac{1}{2 \omega_{1/2}} \frac{d|V_P(n)|^2}{dt} + |V_P(n)|^2 = 2 \Re{V_P(n) V_F(n)} $$
$$ (a, b, c, d) = \arg \min_{\hat{a},\hat{b},\hat{c},\hat{d}} \sum_{n \in N} (|f_{probe}(n; \hat{a},\hat{b}, \hat{c}, \hat{d})|^2 + |f_C(n; \hat{a},\hat{b}, \hat{c}, \hat{d})|^2 + |f_D(n; \hat{a},\hat{b})|^2) $$
其中 $f_{probe}, f_C, f_D$ 分别代表方程的误差项。
现有信号校准方法讨论
- 对角校准:假设有限方向性的影响可以忽略,只使用对角项a和d。
- Pfeiffer等人的方法:使用RF脉冲数据,通过在衰减期间施加额外约束来解决非对角项。
Pfeiffer等人提出的方法主要用于校准超导射频(SRF)腔体的正向和反射信号,特别是在有限隔离度的方向耦合器存在时。该方法特别关注于使用RF脉冲数据,并在信号衰减期间施加额外的约束条件来解决校准矩阵中的非对角项(即b和c项)。
基本原理
在SRF加速器中,正向和反射的RF信号通常通过方向耦合器进行采样。由于方向耦合器的隔离度有限,测量到的正向信号$V_F$和反射信号$V_R$会受到交叉耦合效应的影响。这种交叉耦合会导致信号失真,从而影响腔体参数(如腔体失谐和带宽)的准确估计。
为了校准这些失真,Pfeiffer等人提出使用一个校准矩阵,将测量的信号转换为校准后的信号。校准矩阵的形式如下:
$$V_F = a V_{mF} + b V_{mR}$$
$$V_R = c V_{mF} + d V_{mR}$$
其中,$V_{mF}$和$V_{mR}$分别是测量到的正向和反射信号,$a, b, c, d$是校准参数。
衰减期间的额外约束
Pfeiffer等人的方法关键在于利用RF脉冲的衰减期间的数据来施加额外的约束条件。在衰减期间,假设RF放大器关闭,因此理论上正向信号$V_F$应为零。同时,由于没有新的RF能量输入,反射信号$V_R$应等于腔内的探针信号$V_P$。这些条件可以表示为:
$$V_F(n) = 0 \quad \forall n \in N_{decay}$$
$$V_R(n) = V_P(n) \quad \forall n \in N_{decay}$$
其中,$N_{decay}$是衰减期间的样本索引集合。
优化过程
利用上述约束,可以构建一个优化问题来求解校准参数$a, b, c, d$。优化的目标是最小化校准信号和实际测量信号之间的差异。具体来说,优化问题可以表示为:
$$\min_{a,b,c,d} \sum_{n \in N} \left( |V_F(n) - (a V_{mF}(n) + b V_{mR}(n))|^2 + |V_R(n) - (c V_{mF}(n) + d V_{mR}(n))|^2 \right)$$
在衰减期间,由于$V_F = 0$和$V_R = V_P$,这些条件被直接用于优化过程中,从而提供了额外的约束来解决非对角项。
优点和局限性
优点:
- 利用RF脉冲的衰减期间数据,提供了一种直接且有效的方式来校准正向和反射信号。
- 通过施加额外的约束条件,可以减少参数估计的不确定性,提高校准的准确性。
局限性:
- 该方法假设在衰减期间正向信号完全为零,这在实际应用中可能会受到测量噪声和其他系统误差的影响。
- 对于某些特定的系统配置,如存在额外的反射元件或耦合不完美,该方法可能需要进一步的调整和优化。
总的来说,Pfeiffer等人提出的方法为超导射频腔体的信号校准提供了一种有效的技术手段,尤其适用于需要精确控制和监测加速器性能的场合。
- Brandt的方法:将b、c、d参数表示为a的函数,通过优化问题来计算a。
Brandt的方法是一种针对超导射频(SRF)腔体信号校准的技术,它通过特定的数学模型将非对角项 $ b $ 和 $ c $ 以及 $ d $ 表达为对角项 $ a $ 的函数,进而通过优化问题求解 $ a $。这种方法的核心在于简化校准参数的数量,通过减少参数间的相互依赖来优化校准过程。
基本原理
在SRF腔体的信号校准中,通常需要确定四个参数 $ a, b, c, d $,这些参数构成了校准矩阵,用于将测量的正向 $ V_{mF} $ 和反射 $ V_{mR} $ 信号转换为校准后的信号 $ V_F $ 和 $ V_R $。
$$ V_F = a V_{mF} + b V_{mR} $$
$$ V_R = c V_{mF} + d V_{mR} $$
Brandt的方法提出将 $ b, c, $ 和 $ d $ 表示为 $ a $ 的函数,从而减少需要独立确定的参数数量。具体的表达式为:
$$ b(a) = \frac{a}{z} $$
$$ c(a) = x - a $$
$$ d(a) = \frac{y - a}{z} $$
其中,$ x $ 和 $ y $ 是通过使用对角校准方法得到的 $ a_{diag} $ 和 $ d_{diag} $ 校准系数,而 $ z $ 是通过解决过载线性系统得到的解。
优化问题
Brandt的方法通过最小化一个特定的目标函数来求解 $ a $,该目标函数基于能量守恒原理。优化问题可以表示为:
$$ a = \arg \min_a \left{ \sum_{n \in N} \left[ \frac{d|V_P(n)|^2/dt + |V_P(n)|^2}{2 \omega_{1/2}} - 2 \Re{ V_P(n) V_F(n; a) } \right]^2 \right} $$
其中,$ V_F(n; a) $ 表示使用特定 $ a $ 值校准后的正向信号,$ \omega_{1/2} $ 是腔体的半带宽,$ \Re{} $ 表示取复数的实部,$ N $ 是数据样本的集合。
计算过程
- 初始化:使用对角校准方法确定 $ x $ 和 $ y $。
- **求解 $ z $**:通过解决过载线性系统,找到 $ z $ 的值。
- **优化 $ a $**:使用最小二乘法或其他优化算法,根据上述优化问题求解 $ a $。
- **计算 $ b, c, d $**:根据求得的 $ a $ 值,计算 $ b, c, $ 和 $ d $。
优点和局限性
优点:
- 通过减少需要独立校准的参数数量,简化了校准过程。
- 利用能量守恒原理,提高了校准的物理一致性。
局限性:
- 依赖于对角校准方法得到的 $ x $ 和 $ y $,这可能在某些情况下不够准确。
- $ z $ 的求解可能受到数据质量和系统噪声的影响。
Brandt的方法为SRF腔体的信号校准提供了一种有效的技术手段,尤其适用于需要精确控制和监测加速器性能的场合。通过优化问题求解 $ a $,该方法能够提高校准的精确度和可靠性。
- Qiu等人的方法:针对连续波(CW)操作的校准漂移跟踪,假设z值已知且恒定。
Qiu等人提出的方法专门针对连续波(Continuous Wave, CW)操作中的超导射频(SRF)腔体进行校准漂移跟踪。这种方法的核心在于利用已知且恒定的 $z$ 值来简化校准过程,并适应连续波操作中信号特性的稳定性。
基本原理
在连续波操作模式下,SRF腔体的射频信号相对稳定,这使得可以对校准参数进行跟踪和调整,以补偿可能随时间变化的系统漂移。Qiu等人的方法基于这样的假设:在连续波操作期间,某些系统参数(如耦合器的 $z$ 值)可以认为是恒定的,从而简化了校准过程。
$z$ 值的假设
$z$ 值通常与方向耦合器的S参数有关,它描述了正向信号和反射信号之间的耦合关系。在Qiu等人的方法中,$z$ 值被假设为已知且恒定,这意味着:
$$ z = \frac{a}{b} = \frac{d}{c} $$
其中,$a, b, c, d$ 是校准矩阵中的参数,它们将测量的信号转换为校准后的信号。
校准方法
在连续波操作中,腔体的射频信号变化较小,因此可以利用这一特点来跟踪和调整校准参数。Qiu等人的方法通过最小化一个优化问题来调整校准参数,该优化问题基于以下条件:
$$ \frac{dV_P}{dt} \approx 0 \quad \forall n \in N $$
这表示在连续波操作期间,腔体探针信号 $V_P$ 的变化率接近于零。利用这一条件,可以构建以下优化问题:
$$ a = \arg \min_a \left{ \sum_{n \in N} \left[ \frac{|V_F(n; a) - V_P(n)|^2}{2} \right] \right} $$
其中,$V_F(n; a)$ 表示使用特定 $a$ 值校准后的正向信号。
计算过程
- 初始化:假设 $z$ 值已知且恒定。
- 信号采集:在连续波操作期间,采集腔体探针信号 $V_P$ 和测量的正向信号 $V_{mF}$。
- **优化 $a$**:使用最小二乘法或其他优化算法,根据上述优化问题求解 $a$。
- **计算 $b, c, d$**:根据求得的 $a$ 值和已知的 $z$ 值,计算 $b, c, d$。
优点和局限性
优点:
- 简化了连续波操作中的校准过程,特别是在 $z$ 值已知且恒定的情况下。
- 通过跟踪校准参数的变化,可以适应系统随时间的漂移,提高长期稳定性。
局限性:
- 依赖于 $z$ 值的准确性和稳定性,如果 $z$ 值发生变化,则需要重新校准。
- 在非连续波或信号变化较大的操作模式下,该方法可能不够准确或需要调整。
Qiu等人的方法为连续波操作中的SRF腔体提供了一种有效的校准漂移跟踪技术,尤其适用于需要长期稳定运行的加速器系统。通过利用连续波操作的特点,该方法能够提高校准的效率和可靠性。
基于能量的校准方法推导
基于能量的校准方法是一种利用物理守恒定律(特别是能量守恒)来校准超导射频(SRF)腔体的正向和反射信号的技术。这种方法通过建立一个全局非线性最小二乘优化问题来克服传统校准方法的局限性,如参数估计的不稳定性或对特定操作条件的依赖性。
基本概念
在SRF腔体中,电磁能量的存储和转换可以通过以下动态方程描述:
$$ \frac{d|V_P|^2}{dt} = 2 \Re{V_P^* \frac{dV_P}{dt}} $$
其中,$V_P$ 是腔内的电磁场(探针信号),$\Re{}$ 表示取复数的实部,$\frac{dV_P}{dt}$ 是场的时间导数。
能量守恒方程
考虑到能量守恒,腔内电磁能量的变化率等于正向信号和反射信号功率之差的两倍:
$$ \frac{1}{2 \omega_{1/2}} \frac{d|V_P|^2}{dt} + |V_P|^2 = 2 \Re{V_P V_F} $$
这里,$\omega_{1/2}$ 是腔体的半带宽,$V_F$ 是正向信号。
校准矩阵和优化问题
校准矩阵将测量的信号转换为校准后的信号:
$$ V_F = a V_{mF} + b V_{mR} $$
$$ V_R = c V_{mF} + d V_{mR} $$
其中,$V_{mF}$ 和 $V_{mR}$ 分别是测量的正向和反射信号,$a, b, c, d$ 是需要确定的校准参数。
基于能量守恒的校准方法通过最小化以下目标函数来求解这些参数:
$$ (a, b, c, d) = \arg \min_{\hat{a},\hat{b},\hat{c},\hat{d}} \sum_{n \in N} \left( |f_{probe}(n; \hat{a},\hat{b}, \hat{c}, \hat{d})|^2 + |f_C(n; \hat{a},\hat{b}, \hat{c}, \hat{d})|^2 + |f_D(n; \hat{a},\hat{b})|^2 \right) $$
这里,$f_{probe}, f_C, f_D$ 分别是以下方程的误差项:
- $f_{probe}(n; \hat{a},\hat{b}, \hat{c}, \hat{d}) = V_F(n; \hat{a},\hat{b}) + V_R(n; \hat{c}, \hat{d}) - V_P(n)$:描述了探针信号与校准信号之和与实际探针信号之间的差异。
- $f_C(n; \hat{a},\hat{b}, \hat{c}, \hat{d}) = |V_F(n; \hat{a},\hat{b})|^2 - |V_R(n; \hat{c}, \hat{d})|^2 - C(n)$:描述了正向和反射信号功率之差的平方与能量变化率之间的差异。
- $f_D(n; \hat{a},\hat{b}) = 2\Re{V_P(n) V_F(n; \hat{a},\hat{b})} - D(n)$:描述了校准后的正向信号与探针信号乘积的实部与能量变化率之间的差异。
优化算法
该优化问题通常使用非线性最小二乘算法来求解,如Levenberg-Marquardt算法。这些算法能够迭代地调整参数 $a, b, c, d$,直到找到最小化目标函数的参数值。
优点和局限性
优点:
- 基于物理守恒定律,提高了校准方法的普适性和准确性。
- 通过全局优化,减少了参数估计的不确定性和对特定操作条件的依赖。
局限性:
- 需要精确测量腔内电磁场的时间导数,这可能受到测量噪声的影响。
- 算法的计算复杂度较高,可能需要较长的计算时间。
基于能量的校准方法为SRF腔体提供了一种强大的信号校准工具,尤其适用于需要精确控制和监测的高性能加速器系统。通过利用能量守恒原理,该方法能够提高校准的精确度和可靠性。
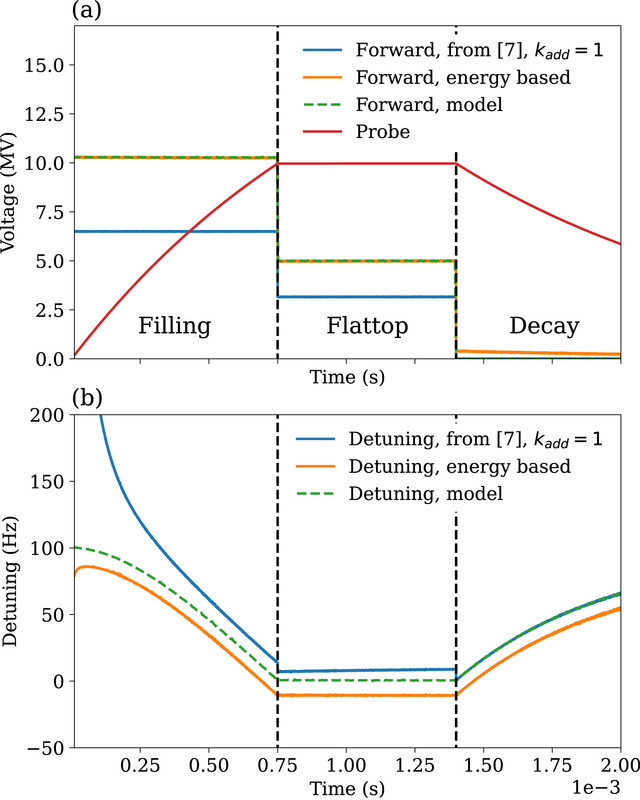
模拟
在论文中,模拟部分是用于验证所提出的基于能量的校准方法的有效性和准确性。模拟环境允许研究者在控制条件下测试算法,无需实际的硬件干预。以下是模拟部分的关键步骤和考虑因素:
模拟环境设置
腔体模型:选择一个特定的SRF腔体模型,如1.3 GHz TESLA型腔体,这是欧洲XFEL加速器中使用的一种常见腔体类型。
参数设定:为模拟设定合适的参数,包括腔体的半带宽 $\omega_{1/2}$、负载品质因数 $Q_L$、以及模拟的脉冲结构(包括填充时间、平顶时间和衰减时间)。
信号生成:生成模拟的正向 $V_{mF}$ 和反射 $V_{mR}$ 信号,这些信号可能包括由RF放大器产生的信号以及由于腔体和传输线之间的耦合而产生的反射信号。
添加噪声:为了模拟真实世界的条件,向模拟信号中添加高斯噪声,模拟测量过程中可能遇到的噪声和不确定性。
模拟过程
信号校准:使用论文中提出的基于能量的校准方法对生成的信号进行校准,计算校准参数 $a, b, c, d$。
性能评估:通过比较校准前后的信号,评估校准方法的性能。这可能包括计算校准信号与真实信号之间的误差、分析校准信号的稳定性和准确性。
参数变化:改变模拟参数(如腔体失谐、耦合强度等),以测试不同条件下校准方法的鲁棒性。
算法比较:将基于能量的校准方法与其他校准方法(如对角校准、Pfeiffer方法、Brandt方法等)进行比较,以展示其优势和潜在的局限性。
分析和优化
误差分析:计算并分析不同校准方法的误差,如均方根误差(RMSE)或平均绝对误差(MAE)。
优化算法参数:调整优化算法中的参数(如初始猜测、权重因子等),以提高校准精度。
讨论结果:基于模拟结果,讨论所提出方法的有效性、准确性和鲁棒性,并与现有方法进行对比。
结果呈现
使用图表和图形来展示校准前后的信号、误差分析结果以及不同方法的性能比较。
详情见论文
模拟部分是验证新方法和算法的重要步骤,它为实验设计和实际应用提供了理论基础和预期结果。
实验
- 在EuXFEL和CryoModule Test Bench (CMTB)上进行了测量。
- 实验结果表明,新方法在高Q负载品质因数的腔体上表现尤为出色。
结论
- 提出的基于能量的校准方法在模拟和实验中均显示出小于1%的校准误差。
- 该方法可能为使用基于模型的技术可靠地执行腔体失超检测提供了新的可能性。
附录:提供Python中校准方法的实现代码
1 | # Copyright 2024 A. Bellandi et al. |