LLRFLibsPy库中loop_analysis函数解读

source code: Github

loop_analysis 函数用于分析控制回路的特性，包括开环传递函数的推导、灵敏度函数和互补灵敏度函数的计算。该函数可以处理连续系统（Ts为None）和离散系统（Ts有一个非零的浮点值）。以下是对该函数的详细解释：

函数参数：

• AG, BG, CG, DG: numpy矩阵（复数），表示被控对象（Plant）模型的状态空间矩阵。
• AK, BK, CK, DK: numpy矩阵（复数），表示控制器的状态空间矩阵。
• Ts: 浮点数，采样时间，单位为秒。如果为None，则为连续系统。
• delay_s: 浮点数，回路延迟时间，单位为秒。
• plot: 布尔值，是否绘制波德图和奈奎斯特图。
• plot_pno: 整数，绘图的点数。
• plot_maxf: 浮点数，要绘制的最大频率范围，单位为赫兹。
• label: 字符串，绘图时的标签。

返回值：

• status: 布尔值，表示函数执行是否成功。
• S_max: 浮点数，最大灵敏度，单位为dB。
• T_max: 浮点数，最大互补灵敏度，单位为dB。

函数流程：

1. 检查输入参数：
   确保plot_pno、plot_maxf和delay_s有合理的默认值。如果定义了Ts，则确保其为正值。

2. 采样频率设定：
   如果Ts为None，则该系统为连续系统，设定采样频率为1。如果Ts不为None，则采样频率fs为1.0/Ts。

3. 级联Plant和控制器得到开环传递函数：
   使用ss_cascade函数将Plant和控制器级联，得到开环传递函数L的状态空间表示（AL, BL, CL, DL）。如果级联失败，返回失败状态。

4. 计算开环传递函数的频率响应：
   使用ss_freqresp函数计算开环传递函数L的频率响应，得到频率响应result_L。如果计算失败，返回失败状态。

5. 应用延迟到开环传递函数：
   频率响应L乘以一个包含延迟的复指数因子，以考虑回路中的延迟。

6. 计算灵敏度和互补灵敏度函数：

   • 灵敏度S: S = 1 / (1 + L)
   • 互补灵敏度T: T = 1 - S

7. 绘图：
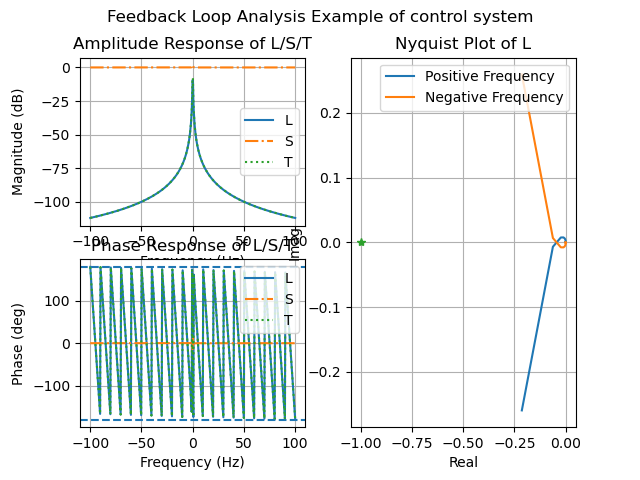
   如果plot为True，调用rf_plot模块中的plot_loop_analysis函数来绘制频率响应图，包括奈奎斯特图和波德图。

8. 计算灵敏度和互补灵敏度的峰值：
   计算灵敏度和互补灵敏度的最大值，单位是dB。

9. 返回结果：
   返回函数执行状态True，以及最大灵敏度S_max和最大互补灵敏度T_max。

总结：

loop_analysis函数是一个用于分析控制回路特性的重要工具。通过计算和绘制控制系统的开环传递函数、灵敏度和互补灵敏度，可以帮助工程师评估系统的稳定性和性能。

示例：

import numpy as np

from set_path import *
from rf_sim import *
from rf_control import *
from rf_calib import *
from rf_sysid import *
from rf_noise import *

# Plant (被控对象) 的状态空间矩阵
AG = np.array([[0, 1], [-2, -3]], dtype=complex)
BG = np.array([[0], [1]], dtype=complex)
CG = np.array([[1, 0]], dtype=complex)
DG = np.array([[0]], dtype=complex)

# 控制器的状态空间矩阵
AK = np.array([[0]], dtype=complex)
BK = np.array([[1]], dtype=complex)
CK = np.array([[1]], dtype=complex)
DK = np.array([[1]], dtype=complex)

# 采样时间（连续系统），设置为None代表连续系统
Ts = None

# 回路延迟时间，单位为秒
delay_s = 0.1

# 是否绘图
plot = True

# 绘图的点数
plot_pno = 500

# 绘制的最大频率范围（Hz）
plot_maxf = 100.0

# 绘图的标签
label = "Example of control system"

# 调用 loop_analysis 函数
status, S_max, T_max = loop_analysis(AG, BG, CG, DG, AK, BK, CK, DK, Ts, delay_s, plot, plot_pno, plot_maxf, label)

# 输出结果
if status:
    print(f"最大灵敏度 S_max: {S_max} dB")
    print(f"最大互补灵敏度 T_max: {T_max} dB")
else:
    print("分析失败")

示例说明：

• 状态空间矩阵：AG, BG, CG, DG 是系统的状态空间矩阵，AK, BK, CK, DK 是控制器的状态空间矩阵。这里已经用简单的例子进行了定义。
• 采样时间：设置为 None 代表连续系统。如果你有离散系统，请设定合适的采样时间。
• 延迟时间：设定为 0.1 秒。
• 绘图参数：你可以设置是否绘图，绘图的点数，以及绘制的最大频率范围。
• 标签：你可以自定义标签以便于识别不同的系统。

最大灵敏度 S_max: 1.6351098604869219 dB
最大互补灵敏度 T_max: -7.837075579929744 dB

运行这段代码后，如果loop_analysis函数执行成功，将会打印出最大灵敏度和最大互补灵敏度的值，并且会绘制出相应的频率响应图。