基于LLRFLibsPy库的基本控制算法示例

Posted on In Views: Disqus:
模拟了一个射频腔（RF cavity）的控制系统，模拟了腔体的激励、响应，以及在不同条件下的反馈控制

source code: Github

这段代码模拟了一个射频腔（RF cavity）的控制系统。具体来说，它模拟了腔体的激励、响应，以及在不同条件下的反馈控制。下面是代码各部分的详细解释：

导入必要的库和模块

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt

from set_path import *
from rf_sim import *
from rf_control import *
from rf_calib import * 
from rf_sysid import *
from rf_noise import *

这段代码导入了NumPy和Matplotlib，用于数值计算和绘图。此外，还导入了一些自定义模块，这些模块提供了射频模拟、控制、校准、系统识别和噪声相关的函数。

定义模拟参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 定义采样频率和其他基本参数
f_scale = 1                         
pi      = np.pi                     
simN    = 2048 * f_scale            

# 腔体参数
fs      = 1e6 * f_scale             
Ts      = 1/fs                      

f0      = 1.3e9                     
roQ     = 1036                      
QL      = 3e6                       
RL      = 0.5 * roQ * QL            
ig      = 0.016                     
ib      = 0.008                     
t_fill  = 510 * f_scale             
t_flat  = 800 * f_scale             
t_bms   = 600 * f_scale             
t_bme   = 1000 * f_scale            

vc0     = 25e6                      
wh      = pi*f0 / QL                
dw      = wh                        

pb_modes = {'freq_offs': [-800e3],              
            'gain_rel':  [-1],                  
            'half_bw':   [2*np.pi*216 * 0.5]}

定义了射频腔体的参数，包括采样频率、操作频率、品质因数等，以及一些时间相关的参数，比如填充时间、平顶时间和束流开始和结束的时间。

计算设定点和前馈

1
2
3
4
5
6
7
status, vc_sp, vf_ff, vb, T = cav_sp_ff(wh, t_fill, t_flat, Ts, 
                                        vc0      = vc0, 
                                        detuning = 0, 
                                        pno      = simN)

vb = np.zeros(simN, dtype = complex)            
vb[t_bms:t_bme] = -RL * ib

使用 cav_sp_ff 函数计算设定点和前馈信号。vb 是束流驱动电压，它在束流开始和结束之间有一个非零值。

添加扰动

1
2
3
dist_freq = 5e3                                         
vf_dist   = vc0 * 0.5 * np.cos(2 * pi * dist_freq * T)  
vf_ff     = vf_ff + vf_dist

在前馈信号中添加一个频率为5kHz的扰动。

定义腔体模型

1
2
3
4
5
6
7
8
9
10
11
result = cav_ss(wh, detuning = dw, passband_modes = pb_modes, plot = False)

status = result[0]
Arf    = result[1]                  
Brf    = result[2]
Crf    = result[3]
Drf    = result[4]
Abm    = result[5]                  
Bbm    = result[6]
Cbm    = result[7]
Dbm    = result[8]

定义腔体的状态空间模型，Arf, Brf, Crf, Drf 是射频驱动的状态空间矩阵，Abm, Bbm, Cbm, Dbm 是束流驱动的状态空间矩阵。

模拟前馈响应

1
2
3
4
5
6
status, T1, vc1, vr1 = sim_ncav_pulse(Arf, Brf, Crf, Drf, vf_ff, Ts,
                                        Abmc = Abm,
                                        Bbmc = Bbm,
                                        Cbmc = Cbm,
                                        Dbmc = Dbm,
                                        vb   = vb)

模拟前馈响应，vc1 是腔体电压的响应。

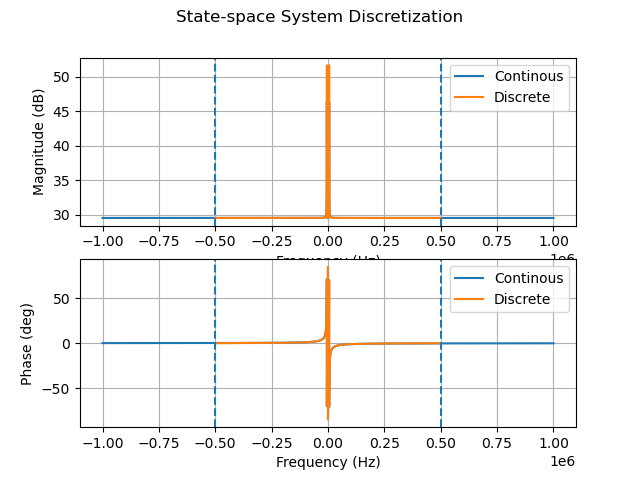
离散化腔体方程

1
2
3
4
5
6
status1, Arfd, Brfd, Crfd, Drfd, _ = ss_discrete(Arf, Brf, Crf, Drf, Ts, 
                                              method = 'zoh', 
                                              plot   = False)
status2, Abmd, Bbmd, Cbmd, Dbmd, _ = ss_discrete(Abm, Bbm, Cbm, Dbm, Ts, 
                                              method = 'bilinear', 
                                              plot   = False)

将腔体的连续时间状态空间模型离散化，用于后续的数字控制。

设计陷波滤波器

1
status, Afd, Bfd, Cfd, Dfd = design_notch_filter(200e3, 4, fs)

设计一个陷波滤波器，用于消除测量中的带通模式。

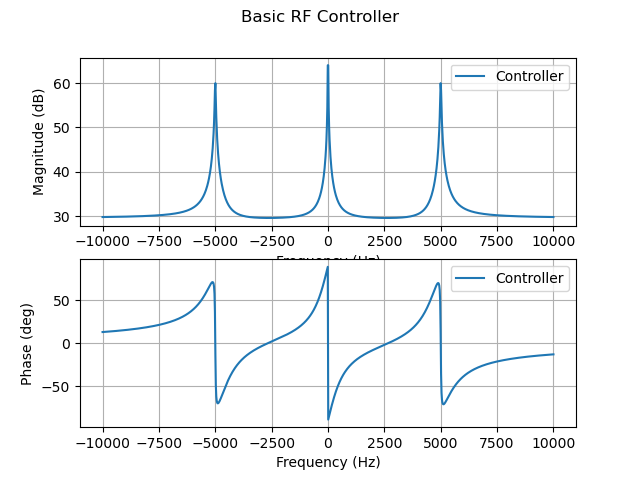
定义反馈控制器

1
2
3
4
5
6
7
8
9
10
11
Kp = 30                                 
Ki = 1e5                                

notches = {'freq_offs': [5e3],          
           'gain':      [1000],
           'half_bw':   [2*np.pi*20]}

status, Akc, Bkc, Ckc, Dkc = basic_rf_controller(Kp, Ki,
                                                 notch_conf = notches,      
                                                 plot       = True, 
                                                 plot_maxf  = 10e3)

定义一个基本的射频控制器，使用比例积分控制（PI控制）和一个带陷波滤波器的反馈回路。

离散化控制器

1
2
3
4
status, Akd, Bkd, Ckd, Dkd, _ = ss_discrete(Akc, Bkc, Ckc, Dkc, Ts, 
                                         method     = 'bilinear', 
                                         plot       = True,
                                         plot_pno   = 10000)

将控制器的连续时间状态空间模型离散化。

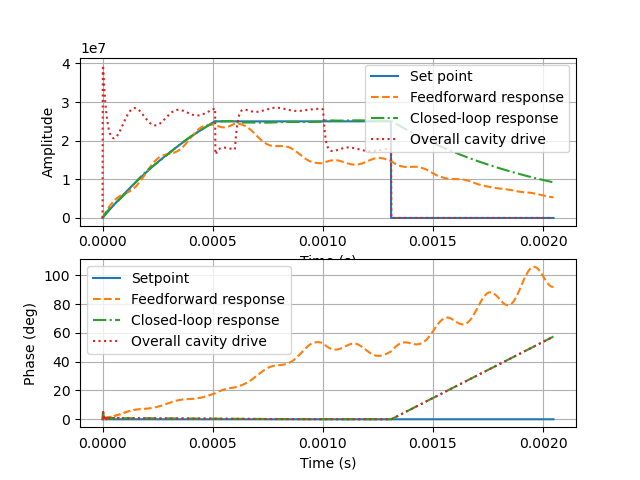
模拟反馈控制回路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
vc2 = np.zeros(simN, dtype = complex)                       
vf2 = np.zeros(simN, dtype = complex)                       

state_rf = np.matrix(np.zeros(Brfd.shape), dtype = complex) 
state_bm = np.matrix(np.zeros(Bbmd.shape), dtype = complex) 
state_k  = np.matrix(np.zeros(Bkd.shape),  dtype = complex) 
state_f  = np.matrix(np.zeros(Bfd.shape),  dtype = complex) 
vf_all = 0.0 + 1j*0.0                                       

for i in range(simN):
    vf2[i] = vf_all

    status, vc2[i], _, state_rf, state_bm = sim_ncav_step(Arfd, Brfd, Crfd, Drfd, vf_all, state_rf,
                                                          Abmd      = Abmd, 
                                                          Bbmd      = Bbmd, 
                                                          Cbmd      = Cbmd, 
                                                          Dbmd      = Dbmd, 
                                                          vb_step   = vb[i],
                                                          state_bm0 = state_bm)

    status, vc_f, state_f = filt_step(Afd, Bfd, Cfd, Dfd, vc2[i], state_f)

    vc_err = vc_sp[i] - vc_f            

    status, vf_all, _, state_k = control_step(Akd, Bkd, Ckd, Dkd, vc_err, state_k, 
                                              ff_step = vf_ff[i])

    vf_all = 0 if (i >= t_fill + t_flat) else vf_all

这段代码模拟了整个反馈控制回路。每个时间步，计算当前的腔体电压，滤波后的电压，误差，然后根据误差更新控制器的输出。

绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
plt.figure();
plt.subplot(2,1,1)
plt.plot(T, np.abs(vc_sp),     label = 'Set point')
plt.plot(T, np.abs(vc1), '--', label = 'Feedforward response')
plt.plot(T, np.abs(vc2), '-.', label = 'Closed-loop response')
plt.plot(T, np.abs(vf2), ':',  label = 'Overall cavity drive')
plt.legend()
plt.grid()
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.subplot(2,1,2)
plt.plot(T, np.angle(vc_sp,deg = True),       label = 'Setpoint')
plt.plot(T, np.angle(vc1,  deg = True), '--', label = 'Feedforward response')
plt.plot(T, np.angle(vc2,  deg = True), '-.', label = 'Closed-loop response')
plt.plot(T, np.angle(vc2,  deg = True), ':',  label = 'Overall cavity drive')
plt.legend()
plt.grid()
plt.xlabel('Time (s)')
plt.ylabel('Phase (deg)')
plt.show(block = False)

最后，绘制了模拟的结果，包括设定点、前馈响应和闭环响应的振幅和相位。

example-feedback-basic-1.png

example-feedback-basic-2.png

example-feedback-basic-3.png