基于LLRFLibsPy库的射频腔外部驱动下的机械响应仿真示例

Posted on In Views: Disqus:
模拟一个射频（RF）腔体在外部驱动和机械模式影响下的响应

这段代码是用于模拟一个射频（RF）腔体在外部驱动和机械模式影响下的响应。以下是对这段代码的详细解读：

导入库和模块

1
2
3
4
5
6
import numpy as np
import matplotlib.pyplot as plt

from set_path import *
from rf_sim import *
from rf_control import *

导入了必要的库和自定义模块，其中 set_path、rf_sim 和 rf_control 是自定义模块，包含了模拟RF腔体和控制的函数。

参数设置

1
2
3
Ts  = 1e-6                  # 电气模型的采样时间，秒
mds = 1                     # 机械模型的降采样因子
Tsm = Ts * mds              # 机械模型的采样时间，秒

设定采样时间，其中 Ts 为电气模型的采样时间，mds 为机械模型的降采样因子，Tsm 为机械模型的采样时间。

定义机械模式并离散化模型

1
2
3
4
5
6
7
8
9
10
mech_modes = {'f': [280, 341, 460, 487, 618],
              'Q': [40, 20, 50, 80, 100],
              'K': [2, 0.8, 2, 0.6, 0.2]}

status, Am, Bm, Cm, Dm = cav_ss_mech(mech_modes)
status, Ad, Bd, Cd, Dd, _ = ss_discrete(Am, Bm, Cm, Dm, 
                                     Ts     = Tsm, 
                                     method = 'zoh', 
                                     plot   = False,
                                     plot_pno = 10000)

定义了机械模式的参数，包括频率 f、品质因数 Q 和增益 K。然后调用 cav_ss_mech 函数生成机械模式的状态空间模型，并使用 ss_discrete 函数将其离散化。

定义腔体参数

1
2
3
4
5
6
7
8
9
10
f0      = 1.3e9                                 # RF 工作频率，Hz
roQ     = 1036                                  # 腔体的 r/Q，欧姆
QL      = 3e6                                   # 负载品质因数
wh      = np.pi * f0 / QL                       # 半带宽，弧度/秒
RL      = 0.5 * roQ * QL                        # 负载电阻（Linac 约定），欧姆
ig      = 0.016                                 # RF 驱动功率等效电流，安培
ib      = 0.008                                 # 平均束流电流，安培
t_fill  = 510                                   # 腔体填充周期长度，样本
t_flat  = 1300                                  # 平顶期结束时间，样本
dw0     = 2*np.pi*000                           # 初始失谐，弧度/秒

定义了腔体的相关参数，如工作频率 f0、腔体的 r/Q、负载品质因数 QL、半带宽 wh、负载电阻 RL、RF 驱动电流 ig、平均束流电流 ib、腔体填充周期长度 t_fill、平顶期结束时间 t_flat 和初始失谐 dw0。

初始化变量

1
2
3
4
5
6
7
8
9
10
11
12
N   = 2048 * 128
vc  = np.zeros(N, dtype = complex)
vf  = np.zeros(N, dtype = complex)
vr  = np.zeros(N, dtype = complex)
vb  = np.zeros(N, dtype = complex)
dw  = np.zeros(N) 

vf[:] = RL * ig * 0.1

state_m  = np.matrix(np.zeros(Bd.shape))        # 机械方程的状态
state_vc = 0.0                                  # 腔体方程的状态
dw_step0 = 0.0

初始化模拟所需的变量。N 为总样本数，vc、vf、vr、vb 和 dw 分别为腔体电压、前向电压、反射电压、束流驱动电压和失谐的数组。state_m 为机械方程的初始状态，state_vc 为腔体方程的初始状态，dw_step0 为初始失谐。

模拟主循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for i in range(N):
    status, vc[i], vr[i], dw[i], state_m = sim_scav_step( wh, 
                                                          dw_step0,
                                                          dw0, 
                                                          vf[i], 
                                                          vb[i], 
                                                          state_vc, 
                                                          Ts, 
                                                          beta      = 1e4,
                                                          state_m0  = state_m, 
                                                          Am        = Ad, 
                                                          Bm        = Bd, 
                                                          Cm        = Cd, 
                                                          Dm        = Dd,
                                                          mech_exe  = True)           
    state_vc = vc[i]
    dw_step0 = dw[i]

通过循环调用 sim_scav_step 函数模拟腔体的响应。在每个时间步 i，计算腔体电压 vc[i]、反射电压 vr[i]、失谐 dw[i] 和机械状态 state_m。然后更新 state_vc 和 dw_step0。

绘制结果

1
2
3
4
5
6
7
8
9
10
11
# 绘制结果
plt.figure()
plt.subplot(2,1,1)
plt.plot(abs(vc) * 1e-6)
plt.xlabel('Time (Ts)')
plt.ylabel('Cavity Voltage (MV)')
plt.subplot(2,1,2)
plt.plot(dw / 2 / np.pi)
plt.xlabel('Time (Ts)')
plt.ylabel('Detuning (Hz)')
plt.show()

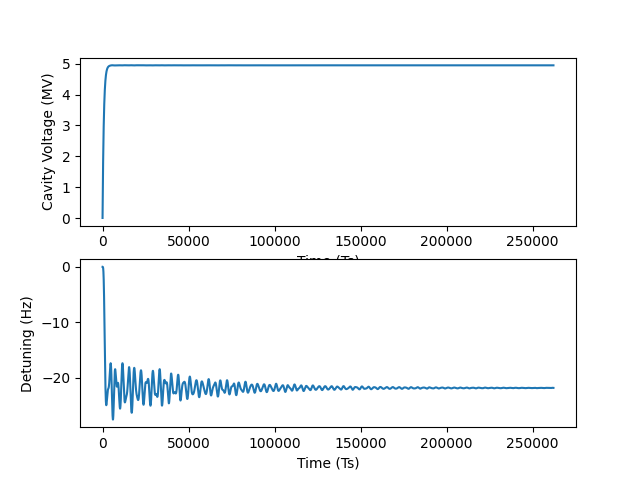
example-sim-cavity-mech.png

绘制腔体电压和失谐随时间的变化。上图显示腔体电压（单位：MV），下图显示失谐（单位：Hz）。