原子核的基本性质（三）

自旋

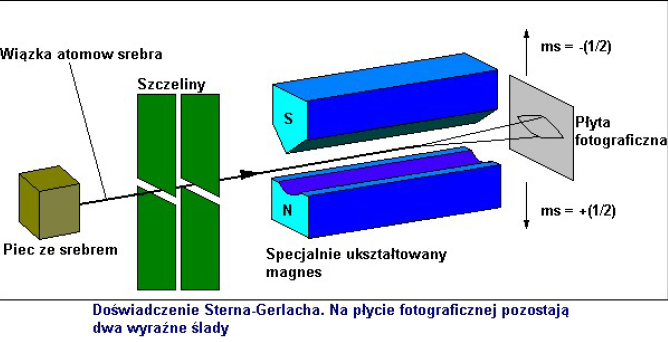
Stern-Gerlach实验

实验原理

• 1922年，Otto Stern和Walther Gerlach进行了以他们名字命名的实验。

• 实验的原理为：

  • 让一束处于基态$(l＝0)$的银原子通过一个不均匀的磁场；

  • 观察其在接收屏上的沉淀痕迹。

    

    

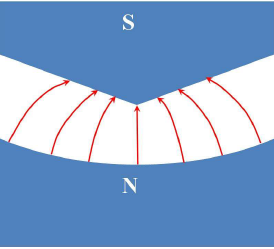
  • 这个实验的特点在于其磁场是一个不均匀的磁场，从而有：

    $$\frac{\partial B_z}{\partial Z}\ne 0$$

实验结果与分析

• 当具有磁矩的粒子束通过磁场时，其将受到磁场对其的作用力：

  $$\vec F = - \nabla(-\vec \mu \cdot \vec B)=(\vec \mu \cdot \nabla)\vec B=\mu_z\frac{\partial B_z}{\partial z}\vec e_z$$

• 对于处于基态的银原子，其轨道角动量量子数$l＝0$，其磁矩也应当为$0$，从而不受力。

• 在接收屏上将观察到一条沉淀痕迹。

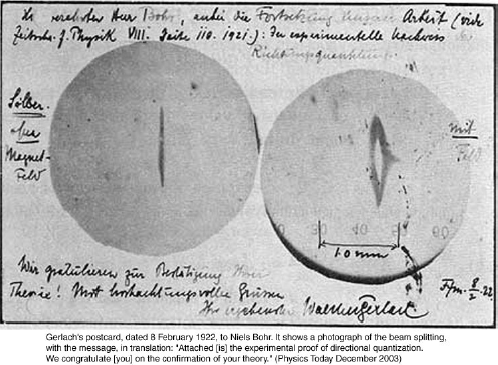
• 实验结果却在接收屏上观察到了两条银原子的沉淀痕迹。

• 这说明，即使银原子处于基态$ (l＝0)$，其磁矩也不为$0$，即有固有(内禀)磁矩。

  

电子的自旋

电子自旋概念的提出

• 针对实验结果与理论分析的矛盾，R. L. Kronig、G. E. Uhlenbeck和S. A. Goudsmit提出了电子自旋的概念。

• 其认为：电子具有内禀角动量，用符号$\hat {\vec S}$表示，其是一个矢量算符：

  $$\hat{\vec S}=\hat{S_x}\vec e_x+\hat{S_y}\vec e_y+\hat{S_z}\vec e_z$$

• 其本征方程为：

  $$\hat{\vec S^2} \left |S,m_s \right \rangle = S(S+1)\hbar^2 \left | S,m_s \right \rangle$$

• $\hat{\vec S}$的大小为：

  $$\sqrt{S(S+1)}\hbar$$

  上式中，$S$为自旋角动量量子数，其值为：

  $$S=\frac{1}{2}$$

• 其在任意方向上（以$z$轴为例）的投影的本征方程为：

  $$\hat{S_z} \left | S,m_s \right \rangle = m_s\hbar \left | S,m_s \right \rangle$$

• $\hat{S_z}$的大小为：

  $$m_s\hbar$$

  上式中，$m_s$称为自旋磁量子数，其取值范围为：

  $$m_s=-S,-S+1,\dots,S-1,S$$

自旋与轨道角动量的耦合

• 电子的角动量将包括轨道角动量和自旋角动量，因此电子的总角动量应当等于二者之和，用符号$\hat{\vec j}$表示：

  $$\hat{\vec j}=\hat{\vec l}+\hat{\vec S}$$

  其也是个矢量算符：

  $$\hat{\vec j} = \hat{j_x}\vec e_x+\hat{j_y}\vec e_y+\hat{j_z}\vec e_z$$

• 其本征方程为：

  $$\hat{\vec j^2} \left | j,m_j \right \rangle = j(j+1)\hbar^2\left |j,m_j \right \rangle$$

• 从而$\hat{\vec j}$的大小为：

  $$\sqrt{j(j+1)}\hbar$$

• $j$的取值范围为：

  $$j=\left | l-S \right |,\left | l-S \right |+1,\dots,l+S$$

• $\hat{\vec j}$在$z$轴上的投影$\hat{j_z}$的本征方程为：

  $$\hat{j_z}\left |j,m_j \right \rangle = m_j\hbar \left |j,m_j \right \rangle$$

• $\hat{j_z}$的大小为：

  $$m_j\hbar$$

• $m_j$为总角动量磁量子数。其取值范围为：

  $$m_j=-j,-j+1,\dots,j-1,j$$

电子的自旋三重态

• 设两个电子的自旋分别记为：$\hat{\vec S_1}$ 和$\hat{\vec S_2}$。记总的自旋角动量$\hat{\vec S}$为：

  $$\hat{S} = \hat{S_1}+\hat{S_2}$$

• 设$\hat{\vec S_1}$和$\hat{\vec S_2}$的量子数分别为$S_1$和$S_2$，则的量子数$S$的取值范围为：

  $$S=S_1+S_2,\dots,\left | S_1-S_2 \right |$$

• 从而$S$的取值只有两种：1和0。

• 当$S＝1$时，$m_s$可以有三个取值：-1，0，1：

  • 当$m_s$取值为$-1$时，其对应状态$\left {\downarrow,\downarrow \right }$；
  • 当$m_s$取值为$0$时，其对应状态$\left {\uparrow,\downarrow \right }$；
  • 当$m_s$取值为$1$时，其对应状态$\left {\uparrow,\uparrow \right }$；

• 此时的情况称为自旋三重态。

• 当$S＝0$时，$m_s$只有一种取值：$0$，其只对应一种状态：$\left {\uparrow,\downarrow \right }$。这种情况称为自旋单态。

自旋的应用

对Stern-Gerlach实验的解释

• 在考虑自旋后，核外电子的总磁矩便为轨道磁矩与自旋磁矩之和：

  $$\hat{\vec \mu_j}=\hat{\vec \mu_s}+\hat{\vec \mu_l}=g_l\frac{e}{2m_e}\hat{\vec l}+g_s\frac{e}{2m_e}\hat{\vec S}$$

  上式中，$g$为电子的$g$因数，其值为：$g_l＝-1$；$g_S＝-2$

• 在磁场中银原子受到的$z$方向的作用力为：

  $$\vec F = \mu_z\frac{\partial B_z}{\partial z}\vec e_z = (g_l \hat{l_z}+g_s \hat{l_z})\frac{e}{2m_e}\cdot \frac{\partial B_z}{\partial z}\vec e_z$$

• 考虑到$\hat{l_z}$和$\hat{S_z}$的取值，并且记：

  $$\mu_B = \frac{e\hbar}{2m_e}$$

• $\mu_B$称为Bohr磁子。

• 因而在$z$方向受到的作用力为：

  $$\vec F = \mu_z\frac{\partial B_z}{\partial z}\vec e_z = (g_l \hat{l_z}+g_s \hat{l_z})\mu_B\cdot \frac{\partial B_z}{\partial z}\vec e_z$$

• 此时对于基态的银原子：

  • 轨道角动量量子数$l＝0$，因而有：$m_l＝0$；
  • 自旋角动量量子数$S＝1/2$，从而有：$m_S＝\pm 1/2$。

• 从而银原子在$z$方向受到的作用力为：

  $$\vec F = \pm \mu_B\frac{\partial B_z}{\partial z}\vec e_z$$

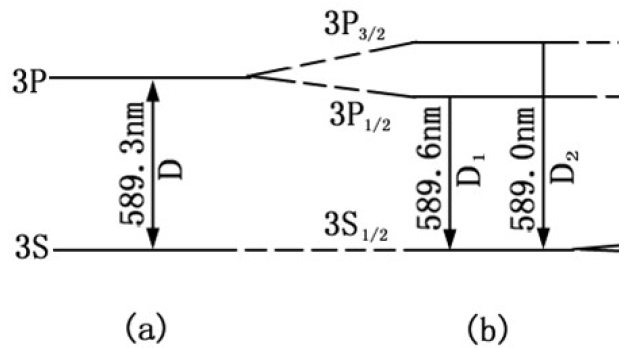
对钠D线精细结构的解释

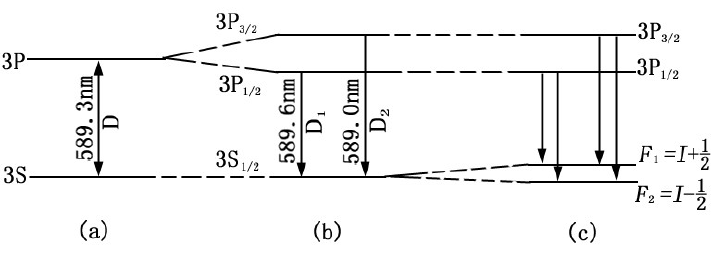
• 钠的光谱中有一条谱线（D线）是核外电子从$3P$能级跃迁到$3S$能级时发出的谱线，波长为$\lambda_D＝589.3nm$。

• 进一步研究发现，其是由波长相差$0.6nm$的两条谱线构成的。其中：$\lambda_1＝589.6nm$，$\lambda_2=589.0nm$。

• 这称为钠D线的精细结构。

  

• 通过电子自旋可以解释钠D线的精细结构。

• 考虑电子的自旋，总角动量便等于：

  $$\hat{\vec j} = \hat{\vec l}+\hat{\vec s}$$

• 根据角动量耦合理论， 的量子数$j$的取值范围为：

  $$j=\left |l-s \right |,\left |l-s \right |+1,\dots,l+s$$

• 这意味着，原来的一个能级将会分裂为多个能级（能级是由量子数确定的）：

  • 对于$3S$能级，其轨道量子数$l＝0$，此时$j＝1/2$，只能取一个值，即仍然只有一个能级；
  • 对于$3P$能级，此时$l＝1$，从而$j$可取两个值：$1/2$或$3/2$。从而原来的一个$3P$能级将分裂为2个：$3P_{1/2}$和$3P_{3/2}$。

• 从而当核外电子从$3S$能级向$3P$能级跃迁时发射的谱线也将随之分裂为2条。

原子核的自旋

钠D线的超精细结构

• 当光谱线的分辨能力进一步提高以后，发现：
  • $D_1$线是由两条间距为$0.0023nm$的谱线组成的；
  • $D_2$线是由两条间距为$0.0021nm$的谱线组成的；
  • 分裂间距大约是$D_1$和$D_2$间距的$1/300$。
• 这个现象称为钠D线的超精细结构。
• 钠D线的超精细结构可以通过引入原子核自旋的概念来进行解释。

原子核的自旋

• 原子核由核子（质子和中子）构成。在原子核中：

  • 核子具有自旋（内禀）角动量；
  • 另一方面由于转动而具有轨道角动量。

• 所有核子的轨道角动量和自旋角动量的矢量和便是原子核的角动量，称为核的自旋。

• 原子核的自旋角动量用符号$\hat{\vec I}$表示，本征方程为：

  $$\hat{\vec P_I^2}\left |I,m_I\right \rangle = I(I+1)\hbar^2 \left| I,m_I\right \rangle$$

• $\hat{\vec I}$的大小为：

  $$\sqrt{I(I+1)}\hbar$$

  上式中，$I$为整数或半整数，称为核的自旋量子数。

• 原子核的自旋在空间任意方向（以$z$轴为例）的投影的本征方程为：

  $$\hat{P_{Iz}}\left |I,m_I\right \rangle = m_I\hbar \left |I,m_I \right \rangle$$

• $\hat{P_{Iz}}$的大小为：

  $$m_I\hbar$$

  上式中，$m_I$称为磁量子数，其取值范围为：

  $$m_I=-I,-I+1,\dots,I-1,I$$

对钠D线超精细结构的解释

• 由于原子核具有自旋，而核外电子也具有总角动量，二者将发生耦合：

  $$\hat{\vec P_F} = \hat{\vec P_I} +\hat{\vec P_j}$$

• 原子的总角动量$\hat{\vec P_F}$的本征方程为：

  $$\hat{\vec P_F^2}\left |F,m_F \right \rangle = F(F+1)\hbar^2\left |F,m_F \right \rangle$$

• $\hat{\vec P_F}$的大小为：

  $$\sqrt{F(F+1)}\hbar$$

  其中，$F$为总角动量量子数，其取值范围为：

  $$F=I+j,I+j-1,\dots,\left |I-j \right |+1,\left |I-j \right |$$

• 显然有：

  • $I \ge j$时，$F$共有$2j＋1$个取值；
  • $I \le j$时，$F$共有$2I＋1$个取值。

• 对于钠的光谱，$3S_{1/2}$能级离原子核最近，其受到原子核自旋的影响最大。此时，电子的总角动量量子数为$j＝1/2$。从而原子的总角动量的取值为：

  $$F=\left | I-\frac{1}{2} \right | \quad or \quad I+\frac{1}{2}$$

• 从而$3S_{1/2}$能级分裂为两个。从而由$3P_{1/2}$能级到$3S_{1/2}$能级跃迁的D1线分为了两条。

• 由$3P_{3/2}$能级到$3S_{1/2}$能级跃迁的D2线因为同样的道理分为了两条。

  

原子核自旋的测量

利用能级数测量原子核自旋

• 原子的总角动量为：

  $$\hat{\vec P_F} = \hat{\vec P_I} + \hat{\vec P_j}$$

• 总角动量量子数$F$的取值范围为：

  $$F=I+j,I+l-1,\dots,\left | I-j \right |$$

• 如果$I \le j$，那么F共有$2I＋1$个值。原来的一个能级将分裂为$2I＋1$个子能级。

• 对于$I\le j$的情况，只要知道子能级的数目，马上就可求出$I$。

• 这种方法对$I$较小的核适用。

• 当$I\ge j$时，无法通过子能级的数目来确定$I$。

间距法

• 根据量子力学，$\hat{\vec P_j}$ 和$\hat{\vec P_I}$的相互作用能$E$正比于$\hat{\vec P_I} \cdot \hat{\vec P_j}$，即：

  $$E=A\hat{\vec P_I} \cdot \hat{\vec P_j}$$

• 根据角动量的耦合关系有：

  $$\hat{\vec P_F^2}=\hat{\vec P_I^2}+\hat{\vec P_j^2}+2\hat{\vec P_I}\cdot\hat{\vec P_j}$$

• 从而有：

  $$\hat{\vec P_I}\cdot\hat{\vec P_j}=\frac{1}{2}(\hat{\vec P_F^2}-\hat{\vec P_I^2}-\hat{\vec P_j^2})$$

  在上式中，$\hat{\vec P_F^2}$的本征值为：

  $$F(F+1)\hbar^2$$

  $\hat{\vec P_I^2}$的本征值为：

  $$I(I+1)\hbar^2$$

  $\hat{\vec P_j^2}$的本征值为：

  $$j(j+1)\hbar^2$$

• 因此可得$\hat{\vec P_I}$和$\hat{\vec P_j}$的相互作用能$E$的本征值为：

  $$E=\frac{1}{2}A\left [F(F+1)-I(I+1)-j(j+1) \right ]\hbar^2$$

• 当$F$有$2j＋1$个值时，相应的$E$也有$2j＋1$个值，对应于$2j＋1$个子能级：

  $$E_1=\frac{1}{2}A\left [(I+j)(I+j+1)-I(I+1)-j(j+1) \right ]\hbar^2$$

  $$E_2=\frac{1}{2}A\left [(I+j-1)(I+j)-I(I+1)-j(j+1) \right ]\hbar^2$$

  $$E_3=\frac{1}{2}A\left [(I+j-2)(I+j-1)-I(I+1)-j(j+1) \right ]\hbar^2$$

  $$\dots$$

• 由此可得，相邻两能级之间的间距为：

  $$\bigtriangleup E_1=E_1-E_2=A\hbar^2(I+j)$$

  $$\bigtriangleup E_2=E_2-E_3=A\hbar^2(I+j-1)$$

  $$\bigtriangleup E_3=E_3-E_4=A\hbar^2(I+j-2)$$

  $$\dots$$

• 从而可得：

  $$\bigtriangleup E_1:\bigtriangleup E_2:\bigtriangleup E_3:\dots=(I+j):(I+j-1):(I+j-2):\dots$$

• 如果从实验上能够测得各个能级之间的间距（即$\bigtriangleup E_i$），那么便可求得$I$值。

• 在实验上发现，Bi的$D_{3/2}$和$S_{1/2}$能级分别分裂为4条和2条。

• 此时能级分裂数等于$2j＋1$，这意味着$I\ge j$。从而无法通过能级分裂数量来确定原子核的自旋。

• 通过实验可以测得$D_{3/2}$的四个子能级之间的间距比为：$6: 5: 4$。从而可得：

  $$(I+j):(I+j-1):(I+j-2)=6:5:4$$

  此时$j＝3/2$，从而可求得Bi原子核的自旋为：

  $$I=9/2$$

• 通过间距法测量原子核的自旋，要求$j\ge 1$。

• 对于$j < 1$的情况，能级间距法无法适用。

相对强度法

• 超精细结构谱线的强度和$2F＋1$成正比：

  $$R \propto 2F+1$$

• 如果设$R_1$和$R_2$分别是谱线$F_1＝I＋j$和$F_2＝I＋j－1$的相对强度，那么有：

  $$\frac{R_1}{R_2}=\frac{2F_1+1}{2F_2+2}=\frac{2(I+j)+1}{2(I+j-1)+1}=\frac{2(I+j)+1}{2(I+j)-1}$$

• 当前面两种方法都不适用时，可以利用这种方法来定出原子核的自旋$I$。

• 对于钠D线的超精细结构，$3S_{1/2}$分裂为两个子能级。此时，D1线的两个条超精细结构谱线的相对强度之比为$5: 3$。从而可得：

  $$\frac{R_1}{R_2}=\frac{2F_1+1}{2F_2+2}=\frac{2(I+j)+1}{2(I+j)-1}=\frac{5}{3}$$

• 从而可得：

  $$I+j=2$$

• 对于钠D1线，$j＝1/2$，从而可得$I＝3/2$。

结论

• 分析原子核自旋的实验数据，可以得到以下两条规律：
  • 偶A核的自旋为整数，其中偶偶核的$I＝0$；
  • 奇A核的自旋为半整数。